Example: ANOVA for Unreplicated Factorials
Use the anova function to carry out an analysis of variance for an unreplicated factorial by detecting a nonsignificant factor and then projecting the factorial into a lower-order factorial.
1. Call the fullfact function to construct a full factorial design matrix for an experiment testing the filtration rate of a pilot plant. The factors A, B, C, and D stand for the temperature, the pressure, the concentration of formaldehyde, and the stirring rate, respectively.
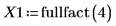
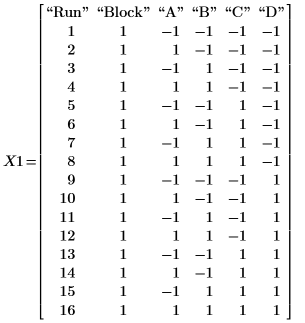
2. Record the results of the experiment in matrix Y1 with one element per each of the sixteen runs.

3. Call the quickscreen function to get the mean response for each main factor.

4. Create an effects plot to determine the significant factors.
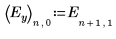
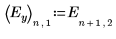

Factor C and the second-order interactions involving C have only a small effect on the experiment. Compared to factors A, B and D, factor C is not significant.
5. Call the anova function to carry out an analysis of variance.
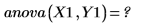
The anova function returns an error because Y1 is unreplicated. However, since C is not significant, “Run 1” and "Run 5" are duplicates as far as factors A, B, and D are concerned. This is also the case for “Run 2" and "Run 6". In fact, the whole ABCD 24 design matrix contains a duplicate of the ABD 23 design matrix when C is not significant.
6. Call the fullfact function to create a 23 full factorial design matrix.

In X2, the factor names are changed. The initial factors A, B, D become A, B, C.
7. Rearrange the experiment results to fit a 23 full factorial experiment.
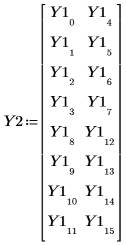
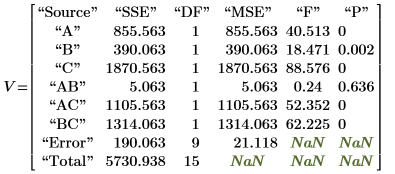
8. Call the anova function using Y2.
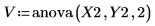
9. Use the qF function to calculate the critical F-value for the factors and interactions and compare their F-value to the critical F-value.
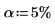
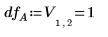
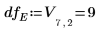
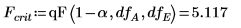
◦ The effect plot shows that factor C is not significant compared to A, B, and D.
◦ Factors A, B, D (shown in V as A, B, C) and their interactions AD, BD (shown in V as AC, BC) are significant at the 5% level since their F-values are greater than Fcrit. This analysis of variance reinforces the subjective conclusion derived from the effects plot.
Reference
Montgomery, D.C., Design and Analysis of Experiments, 5th ed., John Wiley & Sons, New York, 2001, pp. 246.