Elliptic Integral Functions
Elliptic integral functions are a group of integral functions of the following form:
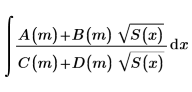
A(m), B(m), C(m) and D(m) are polynomials, and S(x) is a polynomial of degree 3 or 4. Elliptic integral functions are useful in many computational problems, including electromagnetism and gravitation.
You can use elliptic integral functions in the complete or the incomplete form. The complete form calculates the integral from 0 to 1. The incomplete form calculates the integral from 0 to a variable z. You can use the following elliptic integral functions in Mathcad:
• ellipticK—The complete elliptic integral of the first kind:
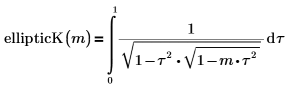
• ellipticF—The incomplete elliptic integral of the first kind:
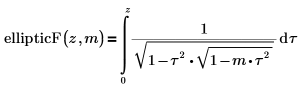
• ellipticE—The complete elliptic integral of the second kind:
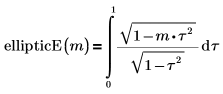
• ellipticE—The incomplete elliptic integral of the second kind:
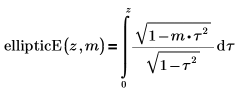
• ellipticPi—The complete elliptic integral of the third kind:
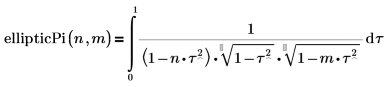
• ellipticPi—The incomplete elliptic integral of the third kind:
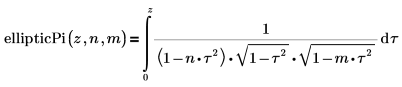
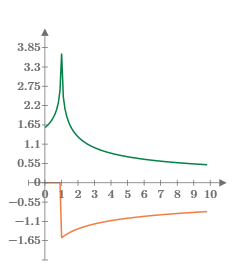
See the behavior of the ellipticK function between 0–10. The result is a real number when 0<m<1, and a complex number if m>1.
The green curve represents the real results, and the orange curve represents the complex results.
Arguments
• m is a scalar or a vector.
• n and z are scalars.