Task 3–5: Working with the Jacobian
The Jacobian is used by some of PTC Mathcad's ODE solvers. With the Jacobian, you can convert variables for multiple integrals. Consider the following region over which you want to integrate a function. The equations for each border are also shown.

1. Define a function to integrate.
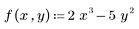
2. Integrate the function over the region. You must divide the integral in two, first integrating over the left-side of the x-y plane, and then over its right-side.
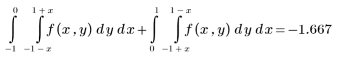
You can introduce new variables to transform the plane and to simplify the integral.
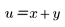
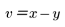
The region of integration for these new variables has borders that are parallel to the axes.

3. Define x and y in terms of u and v.
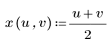
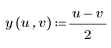
When you convert variables for multiple integrals, you must calculate the Jacobian to scale the integration.
4. Define a vector function F(u, v).
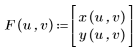
5. Evaluate the Jacobian matrix at a and b.
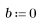
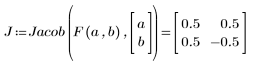
6. Calculate the Jacobian, the determinant of J. Insert the determinant operator.
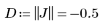
7. Reformulate function f in terms of the new coordinates.
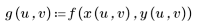
8. Scale the integral with the absolute value of the Jacobian, and evaluate the result.
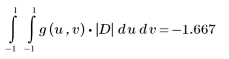
With the new variables, only one integral is needed to integrate the function.
Practice
Before you finish the tutorial, find the time it takes for an object thrown up in the air to reach its highest point. Set up a solve block with the differential equation x’’ = -9.8 and with the initial conditions x(0) = 2 and x’(0) = 3. Set up a second solve block to optimize the function returned by the first solve block.
You can check your answer by plotting the function returned by the first solve block between 0 < t < 1. You can add units as long as you ensure that the units are compatible throughout your calculations.
Congratulations! You have completed the Solving Tutorial.