Task 2–3: Nonlinear Least Squares Fitting
Fit the parameters of a function that models a data set. Use a solve block to minimize the residuals between the data set and the fitted function. As with other optimization problems, you can also rearrange the problem to look for a root. Here, set the residuals to zero.
1. Define a data set.
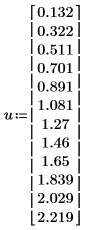

2. Define a fitting function, the Weibull, with unknown parameters α and β.
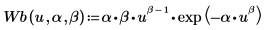
3. Define the residuals, the difference between the v values from the data set and the v values calculated with Wb.
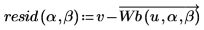
4. Define the sum of squares.
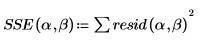
5. To find the parameters α and β that best fit the Weibull function, insert a solve block, define guess values for α and β, and then call the minimize function.

6. Evaluate the solution.
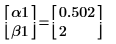
7. Calculate the mean squared error. This value is zero when a true solution exists.
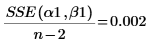
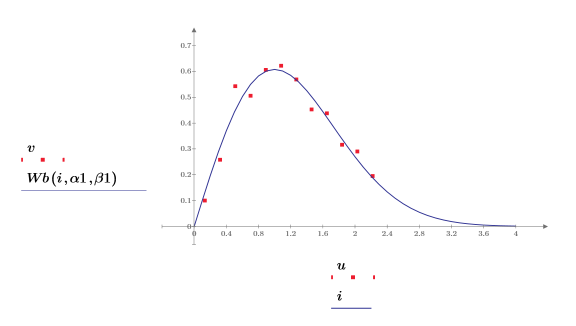
8. Plot the data set and the fitted Weibull function.
9. To fit the parameters using the constraint resid = 0, use the minerr function instead of the minimize function.
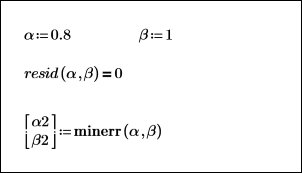
You cannot use the find function here because there is no exact solution for α2 and β2. An error is returned to indicate that no solution exists. The minerr function works the same way as the find function, except that it returns an approximate solution if it fails to converge to the solution within a set number of iterations.
10. Calculate the mean squared error for the new parameters.
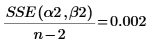
11. Compare the results returned by minimize and by minerr.
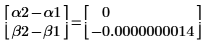
Practice
Before you move on to the next exercise, find the price for an item assuming that you want to maximize profit, n ∙ p. The relationship between the number of items sold and the price is described by the function n:
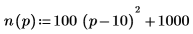
Plot the profit function for 0 < p < 10 before choosing a guess value.