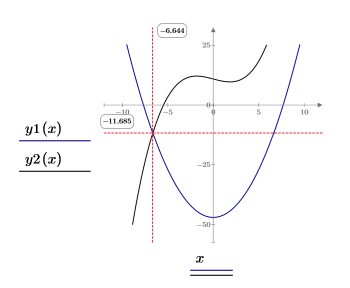
Task 1–2: Nonlinear System of Equations
As seen in the previous task, solve blocks provide a natural environment for easily defining problems. Solve blocks are more general than solvers or matrix calculation. For example, find the coordinates of the crossing point of two nonlinear functions.
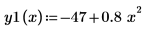
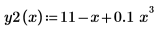

Solving with a Solve Block
1. Press Ctrl+1 to insert a solve block region, and then insert the following items:
◦ The definition of functions y1 and y2
◦ Guess values for the coordinates of the crossing point based on the graph
◦ Two constraints for the two unknowns
◦ The solve block function find, automatically assigned the keyword label

Solving with a Solver
Recall the functions y1 and y2:
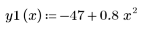
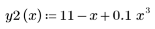
You can define a new function f(x) = y2(x) - y1(x).
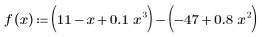
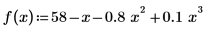
The newly defined function f crosses the x-axis at the same x value as the crossing point of the nonlinear functions. f is a polynomial, so you can use the polyroots function instead of the more general root solver to find where f crosses the x-axis.
1. Assign the polynomial coefficients to vector c. The first element of c is the intercept and the next elements are the coefficients for each power of x, in ascending order.
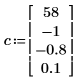
2. Call the polyroots function.
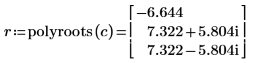
• The polyroots function returns a vector of all real and complex solutions, and the real solutions are listed first. • On the other hand, solve blocks return one solution at a time. To find other solutions, you must try other guess values. |
3. Calculate the horizontal and vertical coordinates of the intersection point (h, v).
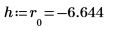
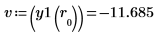
4. Use a vertical and a horizontal marker to show the intersection point on the plot.