Polynomfunktionen

Funktionen > Spezielle Funktionen > Weitere spezielle Funktionen > Polynomfunktionen

Polynomfunktionen

Die folgenden Funktionen übergeben den Wert des aufgelisteten Polynoms vom Grad n bei x:

• Her(n, x) – Hermite-Polynom oder die Lösung der folgenden Gleichung:

<region id="ID0EGPFAB" top="76.800000000000011" left="57.600000000000009" height="52.369333557128911" width="196.435" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="11">
    <apply xmlns="http://schemas.mathsoft.com/math50">
      <equal />
      <apply>
        <plus />
        <apply>
          <minus />
          <apply>
            <derivative />
            <lambda>
              <boundVars>
                <id xml:space="preserve">x</id>
              </boundVars>
              <id xml:space="preserve">y</id>
            </lambda>
            <degree>
              <real>2</real>
            </degree>
          </apply>
          <apply>
            <mult />
            <apply>
              <scale />
              <real>2</real>
              <id xml:space="preserve">x</id>
            </apply>
            <apply>
              <derivative />
              <lambda>
                <boundVars>
                  <id xml:space="preserve">x</id>
                </boundVars>
                <id xml:space="preserve">y</id>
              </lambda>
              <degree>
                <placeholder />
              </degree>
            </apply>
          </apply>
        </apply>
        <apply>
          <scale />
          <real>2</real>
          <id xml:space="preserve">ny</id>
        </apply>
      </apply>
      <real>0</real>
    </apply>
  </math>
</region>

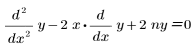
• Lag(n, x) – LaGuerre-Polynom oder die Lösung der folgenden Gleichung:

<region id="ID0EXQFAB" top="134.40000000000003" left="57.600000000000009" height="52.369333557128911" width="222.12833333333333" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="13">
    <apply xmlns="http://schemas.mathsoft.com/math50">
      <equal />
      <apply>
        <plus />
        <apply>
          <plus />
          <apply>
            <mult />
            <id xml:space="preserve">x</id>
            <apply>
              <derivative />
              <lambda>
                <boundVars>
                  <id xml:space="preserve">x</id>
                </boundVars>
                <id xml:space="preserve">y</id>
              </lambda>
              <degree>
                <real>2</real>
              </degree>
            </apply>
          </apply>
          <apply>
            <mult />
            <parens>
              <apply>
                <minus />
                <real>1</real>
                <id xml:space="preserve">x</id>
              </apply>
            </parens>
            <apply>
              <derivative />
              <lambda>
                <boundVars>
                  <id xml:space="preserve">x</id>
                </boundVars>
                <id xml:space="preserve">y</id>
              </lambda>
              <degree>
                <placeholder />
              </degree>
            </apply>
          </apply>
        </apply>
        <id xml:space="preserve">ny</id>
      </apply>
      <real>0</real>
    </apply>
  </math>
</region>

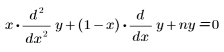
• Leg(n, x) – Legendre-Polynom oder die Lösung der folgenden Gleichung:

<region id="ID0EISFAB" top="192.00000000000003" left="57.600000000000009" height="52.369333557128911" width="295.66166666666669" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="15">
    <apply xmlns="http://schemas.mathsoft.com/math50">
      <equal />
      <apply>
        <plus />
        <apply>
          <minus />
          <apply>
            <mult />
            <parens>
              <apply>
                <minus />
                <real>1</real>
                <apply>
                  <pow />
                  <id xml:space="preserve">x</id>
                  <real>2</real>
                </apply>
              </apply>
            </parens>
            <apply>
              <derivative />
              <lambda>
                <boundVars>
                  <id xml:space="preserve">x</id>
                </boundVars>
                <id xml:space="preserve">y</id>
              </lambda>
              <degree>
                <real>2</real>
              </degree>
            </apply>
          </apply>
          <apply>
            <mult />
            <apply>
              <scale />
              <real>2</real>
              <id xml:space="preserve">x</id>
            </apply>
            <apply>
              <derivative />
              <lambda>
                <boundVars>
                  <id xml:space="preserve">x</id>
                </boundVars>
                <id xml:space="preserve">y</id>
              </lambda>
              <degree>
                <placeholder />
              </degree>
            </apply>
          </apply>
        </apply>
        <apply>
          <scale />
          <apply>
            <id xml:space="preserve">n</id>
            <apply>
              <plus />
              <id xml:space="preserve">n</id>
              <real>1</real>
            </apply>
          </apply>
          <id xml:space="preserve">y</id>
        </apply>
      </apply>
      <real>0</real>
    </apply>
  </math>
</region>

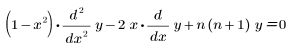
• Tcheb(n, x) – Tschebyscheff-Polynom der ersten Art oder die Lösung der folgenden Gleichung:

<region id="ID0EZTFAB" top="249.60000000000002" left="57.600000000000009" height="52.369333557128911" width="241.09166666666667" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="17">
    <apply xmlns="http://schemas.mathsoft.com/math50">
      <equal />
      <apply>
        <plus />
        <apply>
          <minus />
          <apply>
            <scale />
            <parens>
              <apply>
                <minus />
                <real>1</real>
                <apply>
                  <pow />
                  <id xml:space="preserve">x</id>
                  <real>2</real>
                </apply>
              </apply>
            </parens>
            <apply>
              <derivative />
              <lambda>
                <boundVars>
                  <id xml:space="preserve">x</id>
                </boundVars>
                <id xml:space="preserve">y</id>
              </lambda>
              <degree>
                <real>2</real>
              </degree>
            </apply>
          </apply>
          <apply>
            <mult />
            <id xml:space="preserve">x</id>
            <apply>
              <derivative />
              <lambda>
                <boundVars>
                  <id xml:space="preserve">x</id>
                </boundVars>
                <id xml:space="preserve">y</id>
              </lambda>
              <degree>
                <placeholder />
              </degree>
            </apply>
          </apply>
        </apply>
        <apply>
          <scale />
          <apply>
            <pow />
            <id xml:space="preserve">n</id>
            <real>2</real>
          </apply>
          <id xml:space="preserve">y</id>
        </apply>
      </apply>
      <real>0</real>
    </apply>
  </math>
</region>

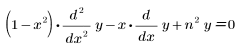
• Ucheb(n, x) – Tschebyscheff-Polynom der zweiten Art oder die Lösung der folgenden Gleichung:

<region id="ID0EKVFAB" top="307.20000000000005" left="57.600000000000009" height="52.369333557128911" width="292.11166666666668" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="19">
    <apply xmlns="http://schemas.mathsoft.com/math50">
      <equal />
      <apply>
        <plus />
        <apply>
          <minus />
          <apply>
            <scale />
            <parens>
              <apply>
                <minus />
                <real>1</real>
                <apply>
                  <pow />
                  <id xml:space="preserve">x</id>
                  <real>2</real>
                </apply>
              </apply>
            </parens>
            <apply>
              <derivative />
              <lambda>
                <boundVars>
                  <id xml:space="preserve">x</id>
                </boundVars>
                <id xml:space="preserve">y</id>
              </lambda>
              <degree>
                <real>2</real>
              </degree>
            </apply>
          </apply>
          <apply>
            <mult />
            <apply>
              <scale />
              <real>3</real>
              <id xml:space="preserve">x</id>
            </apply>
            <apply>
              <derivative />
              <lambda>
                <boundVars>
                  <id xml:space="preserve">x</id>
                </boundVars>
                <id xml:space="preserve">y</id>
              </lambda>
              <degree>
                <placeholder />
              </degree>
            </apply>
          </apply>
        </apply>
        <apply>
          <scale />
          <apply>
            <id xml:space="preserve">n</id>
            <apply>
              <plus />
              <id xml:space="preserve">n</id>
              <real>2</real>
            </apply>
          </apply>
          <id xml:space="preserve">y</id>
        </apply>
      </apply>
      <real>0</real>
    </apply>
  </math>
</region>

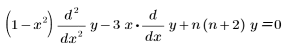
• Jac(n, a, b, x) – Jacobi-Polynom mit den Parametern a und b oder die Lösung der folgenden Gleichung:

<region id="ID0EDXFAB" top="364.80000000000007" left="57.600000000000009" height="52.369333557128911" width="448.05166666666668" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="21">
    <apply xmlns="http://schemas.mathsoft.com/math50">
      <equal />
      <apply>
        <plus />
        <apply>
          <plus />
          <apply>
            <scale />
            <parens>
              <apply>
                <minus />
                <real>1</real>
                <apply>
                  <pow />
                  <id xml:space="preserve">x</id>
                  <real>2</real>
                </apply>
              </apply>
            </parens>
            <apply>
              <derivative />
              <lambda>
                <boundVars>
                  <id xml:space="preserve">x</id>
                </boundVars>
                <id xml:space="preserve">y</id>
              </lambda>
              <degree>
                <real>2</real>
              </degree>
            </apply>
          </apply>
          <apply>
            <scale />
            <parens>
              <apply>
                <minus />
                <apply>
                  <minus />
                  <id xml:space="preserve">b</id>
                  <id xml:space="preserve">a</id>
                </apply>
                <apply>
                  <scale />
                  <parens>
                    <apply>
                      <plus />
                      <apply>
                        <plus />
                        <id xml:space="preserve">a</id>
                        <id xml:space="preserve">b</id>
                      </apply>
                      <real>2</real>
                    </apply>
                  </parens>
                  <id xml:space="preserve">x</id>
                </apply>
              </apply>
            </parens>
            <apply>
              <derivative />
              <lambda>
                <boundVars>
                  <id xml:space="preserve">x</id>
                </boundVars>
                <id xml:space="preserve">y</id>
              </lambda>
              <degree>
                <placeholder />
              </degree>
            </apply>
          </apply>
        </apply>
        <apply>
          <scale />
          <apply>
            <id xml:space="preserve">n</id>
            <apply>
              <plus />
              <apply>
                <plus />
                <apply>
                  <plus />
                  <id xml:space="preserve">n</id>
                  <id xml:space="preserve">a</id>
                </apply>
                <id xml:space="preserve">b</id>
              </apply>
              <real>1</real>
            </apply>
          </apply>
          <id xml:space="preserve">y</id>
        </apply>
      </apply>
      <real>0</real>
    </apply>
  </math>
</region>

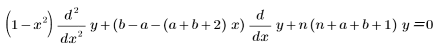
Das Tschebyscheff- und das Legendre-Polynom sind Sonderfälle des Jacobi-Polynoms.

Argumente

• n ist eine nicht negative Ganzzahl.

• x ist ein reeller Skalar.

• a, b sind reelle Skalare größer als –1.

Zugehörige Themen

Weitere spezielle Funktionen

Beispiel: Polynomfunktionen

War dies hilfreich?