GDG-Funktion
• odesolve(vf, b, [intvls]) – Definiert eine Funktion, die die Lösung eines Systems gewöhnlicher Differentialgleichungen darstellt, für das eine Anfangswert- oder eine Randwertbedingung gilt. Die gewöhnlichen Differentialgleichungen müssen in ihrem höchsten Ableitungsterm linear sein, und die Anzahl der Anfangs- und Randbedingungen muss gleich den Ordnungen der Differentialgleichungen sein.
Argumente
• vf ist eine Funktion oder ein Spaltenvektor von Funktionen, die innerhalb des Lösungsblocks erscheinen.
Wenn Sie die Funktionen in vf definieren, müssen Sie die Liste der Argumente angeben. Wenn Sie z.B. die Funktionen f(t) und g(t) lösen, geben Sie vf wie folgt ein:
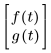
• b ist der reelle Endpunkt des Integrationsintervalls. b kann größer als oder kleiner als der Anfangswert sein, der im Lösungsblock definiert ist.
• intvls (optional) ist die Ganzzahl der Diskretisierungsintervalle, die zum Interpolieren der Lösungsfunktion verwendet werden. Die Anzahl der Lösungspunkte ist gleich der Anzahl der Intervalle +1. Der Standardwert für intvls beträgt 1000.
Der Standardwert von intvls ist in der Regel groß genug, um eine genaue interpolierte Lösung zu liefern. Sie können den Wert jedoch erhöhen, wenn Sie mit der Lösung kleine Details erfassen möchten. Dazu muss odesolve jedoch mehr Punkte für die Interpolation speichern, wodurch sich ggf. die Berechnungszeit erhöht.
Wenn Sie eine GDG über ein großes Intervall lösen, legen Sie für intvls einen Wert fest, der größer ist als der Standardwert.
Einheiten und Dimensionen
Einheiten können in odesolve-Funktionen und Randbedingungen verwendet werden. Für Einheiten und Dimensionen gelten folgende Regeln:
• Dimensionen müssen während des gesamten Lösungsprozesses konsistent sein. Wenn t aus argumentDimension und f(t) aus valueDimension ist,
dann
muss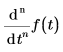 
aus valueDimensions/argumentDinemsionsn sein.
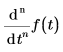aus valueDimensions/argumentDinemsionsn sein.Beispiel: t ist in Sekunden und f(t) ist in Metern, dann
ist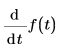 
in m/s und
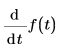in m/s und
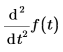ist in m/s2.• Der Anfangswert und der Endpunkt des Integrationsintervalls müssen dieselbe Dimension wie das Funktionsargument aufweisen.
• Die Anzahl der Diskretisierungsintervalle ist immer einheitenlos.
Zusätzliche Informationen
• Die Funktion odesolve kann nur innerhalb eines Lösungsblocks verwendet werden.
• Die PTC Mathcad Legacy-Funktion Odesolve kann durch ihr Gegenstück mit kleinem Anfangsbuchstaben ausgetauscht werden.
• Wenn die Funktion mit kleinem Anfangsbuchstaben über die Multifunktionsleiste eingefügt oder die Version mit Klein-/Großbuchstaben manuell eingegeben wird, wird ihr automatisch die Beschriftung Schlüsselwort zugewiesen.
• Die Funktion odesolve verwendet den Adams/BDF-Lösungsalgorithmus.
• Innerhalb eines Lösungsblocks wird odesolve nicht vom TOL-Wert beeinflusst.