Lambert-Funktionen
• LambertW(x) – Gibt den Hauptwert der Funktion LambertW zurück, W0.
Für die LambertW Funktion gilt die Beziehung:
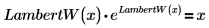
• LambertW(n, x) – Gibt den n-ten Zweig von LambertW als Funktion in der komplexen Fläche zurück.
Zwischen LambertW(x) und LambertW(n, x) besteht folgende Beziehung:
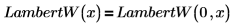
Argumente
• x ist ein reeller oder komplexer Skalar oder ein Vektor.
• n ist eine Ganzzahl oder ein Vektor von Ganzzahlen der gleichen Größe wie x. Wenn x ein Skalar ist, kann n ein Vektor beliebiger Größe sein. Wenn dieser Wert nicht angegeben wird, ist n standardmäßig 0.
Zusätzliche Informationen
• Der Hauptzweig W0(x) ist ein reeller Wert im Bereich -1/e ≤ x.
• Der -1-Zweig W-1(x) ist ebenfalls ein reeller Wert im Bereich -1/e ≤ x < 0.