Sinusintegral und Kosinus-verjüngtes-Fenster
• Si(x) – Die Sinusintegralfunktion wird wie folgt definiert:
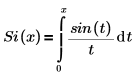
Die Darstellung der Reihenentwicklung lautet:
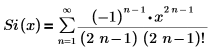
Das angezeigte Ergebnis stellt drei der vorgegebenen sechs Ausdrücke der Reihe dar, die keine Koeffizienten von 0 haben.
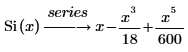
• Ci(x) – Die Fresnel-Kosinusintegralfunktion wird wie folgt definiert:
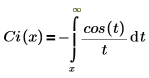
Eine andere Form der Definition ist:
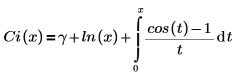
Die Darstellung der Reihenentwicklung lautet:
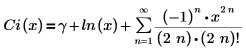
Die letzten beiden Ausdrücke stellen zwei der vorgegebenen sechs Ausdrücke der Reihe dar, die keine Koeffizienten von 0 haben.
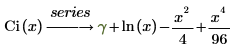
• Shi(x) – Die hyperbolische Sinusintegralfunktion wird wie folgt definiert:
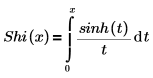
Das angezeigte Ergebnis stellt drei der vorgegebenen sechs Ausdrücke der Reihe dar, die keine Koeffizienten von 0 haben.
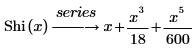
Die Ausdrücke der Reihenentwicklung der Funktionen Si und Shi sind mit Ausnahme der Zeichen der Ausdrücke, für die n gerade ist, identisch.
• Chi(x) – Die hyperbolische Kosinusintegralfunktion wird wie folgt definiert:
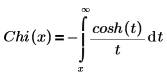
Eine andere Form der Definition ist:
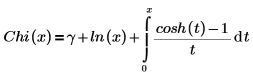
Die letzten beiden Ausdrücke stellen zwei der vorgegebenen sechs Ausdrücke der Reihe dar, die keine Koeffizienten von 0 haben.
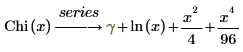
Die Ausdrücke der Reihenentwicklung der Funktionen Ci und Chi sind mit Ausnahme der Zeichen der Ausdrücke, für die n ungerade ist, identisch.
Argumente
• x ist ein reeller oder komplexer Skalar oder ein Vektor von reellen oder komplexen Skalaren.
Zusätzliche Informationen
Diese Funktionen sind hilfreich, wenn Sie das Schlüsselwort float verwenden, das Funktionen numerisch auswertet, anstatt symbolische Berechnungen zurückzugeben.