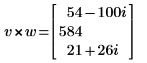Beispiel: Vektoralgebra
1. Definieren Sie einen Vektor, und zeigen Sie seine vereinfachte Form an.
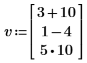
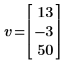
2. Fügen Sie einen komplexen Vektor zu v hinzu.
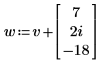
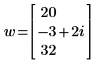
3. Ermitteln Sie den negativen Vektor w.
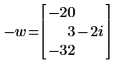
4. Multiplizieren Sie den Vektor wmit einem Skalar.
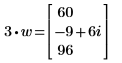
5. Addieren Sie die Komponenten des Vektors v. Drücken Sie Ctrl+Shift+$, um den Summationsoperator einzufügen.
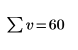
Dies entspricht der folgenden Berechnung: 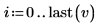 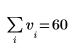 |
6. Ermitteln Sie den Betrag des Vektors w. Drücken Sie Ctrl+Shift+|, um den Operator Norm einzufügen.
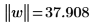
Dies entspricht der folgenden Berechnung: 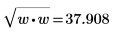 |
7. Transponieren Sie den Vektor w. Drücken Sie Ctrl+Shift+T, um den Transponieroperator einzufügen.
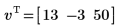
8. Ermitteln Sie die konjugiert komplexe Zahl des Vektors w. Drücken Sie Ctrl+Shift+_, um den Operator für konjugiert komplexe Zahlen einzufügen.
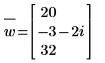
9. Berechnen Sie das Skalarprodukt der Vektoren v und w.
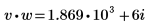
Das Skalarprodukt wird berechnet, indem jedes Element des ersten Vektors mit dem entsprechenden Element der konjugiert komplexen Zahl des zweiten Vektor multipliziert und die Ergebnisse anschließend summiert werden.
10. Berechnen Sie das Kreuzprodukt der Vektoren v und w. Drücken Sie Ctrl+8, um den Vektorprodukt-Operator einzufügen.