Beispiel: Einheiten mit den polynomischen Interpolationsfunktionen verwenden

Funktionen > Datenanalyse > Interpolation und Vorhersage > Beispiel: Einheiten mit den polynomischen Interpolationsfunktionen verwenden

1. Definieren Sie zwei Eingabevektoren und eine unabhängige Variable.

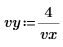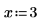2. Legen Sie die Einheiten fest.

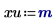
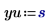
3. Werten Sie die Eingabevektoren und die Eingabevariable aus.

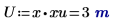Die Einheit der unabhängigen Variable U muss der Einheit des ersten Argumentvektors entsprechen.

Polynominterpolation

1. Verwenden Sie die Funktion polyint, um die Interpolationsfunktion an den angegebenen unabhängigen variablen Werten auszuwerten.

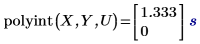
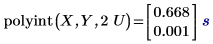
Die Suche nach U im Eingabevektor X führt zu einer Entsprechung, und der entsprechende genaue Wert im Vektor Y ist 1.333 mit einem Fehler von Null. 2U hat jedoch keine genaue Entsprechung in X, und dies ergibt einen interpolierten Wert mit einem Fehler ungleich null.

2. Verwenden Sie die Funktion length, um die Länge der Eingabevektoren zu bestimmen. Erstellen Sie anschließend ein kurzes Programm, um die Interpolationsfunktionen an unterschiedlichen Punkten auszuwerten. Zeigen Sie die interpolierten Punkte in der ersten Spalte und die Fehlerwerte in der zweiten Spalte an.

<region id="ID0ETNMU" actualWidth="485.86333333333334" actualHeight="197.304" top="1075.2000000000003" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
 <math resultRef="45">
 <define xmlns="http://schemas.mathsoft.com/math50">
 <id labels="VARIABLE" xml:space="preserve">M</id>
 <eval>
 <program>
 <for>
 <id labels="VARIABLE" xml:space="preserve">u</id>
 <range>
 <real>0</real>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">L</id>
 </range>
 <program>
 <for>
 <id labels="VARIABLE" xml:space="preserve">v</id>
 <range>
 <real>0</real>
 <real>1</real>
 </range>
 <program>
 <localDefine>
 <apply>
 <indexer />
 <id labels="VARIABLE" xml:space="preserve">M</id>
 <sequence>
 <id labels="*" xml:space="preserve">u</id>
 <id labels="*" xml:space="preserve">v</id>
 </sequence>
 </apply>
 <apply>
 <indexer />
 <parens>
 <apply>
 <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">polyint</id>
 <sequence>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">X</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">Y</id>
 <apply>
 <mult />
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">u</id>
 <id labels="UNIT" xml:space="preserve">m</id>
 </apply>
 </sequence>
 </apply>
 </parens>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">v</id>
 </apply>
 </localDefine>
 </program>
 </for>
 </program>
 </for>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">M</id>
 </program>
 <unitOverride>
 <placeholder />
 </unitOverride>
 </eval>
 </define>
 <resultFormat>
 <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
 </resultFormat>
 </math>
</region>

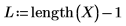
Die Variable u muss ein Skalar sein, und die Einheit m wird als ein Teil des Funktionsarguments hinzugefügt.

3. Speichern Sie die Interpolationspunkte und die Fehlerwerte in zwei unabhängigen Vektoren.

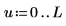
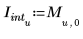
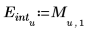
4. Plotten Sie die Interpolationspunkte zusammen mit dem Fehlerarbeitsraum.

<region id="ID0E3RMU" actualWidth="576" actualHeight="307.2" top="1401.6000000000001" left="38.400000000000006" height="307.2" width="576" xmlns="http://schemas.mathsoft.com/worksheet50">
 <plot background-type="white" origin-positioning="true">
 <xyPlot>
 <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
 <legend />
 <traces>
 <trace resultRef="49">
 <traceStyle color="#FFED1D2F" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
 </trace>
 <trace resultRef="50">
 <traceStyle color="#FF068149" symbol="none" line-weight="1" line-style="Dash">Linien</traceStyle>
 </trace>
 <trace resultRef="51">
 <traceStyle color="#FF2E3192" symbol="none" line-weight="1" line-style="Dash">lines</traceStyle>
 </trace>
 </traces>
 <graph-size width="418.4" height="230.4" />
 <axes>
 <xAxis rank="1" legend-position="PlotBoundaryBottom" start="0" end="9">
 <axisLine position="origin" positionticmark="0" legendWidth="61.21" />
 <axisGrid>
 <gridFrequency>11</gridFrequency>
 <gridLabels display="true" />
 <gridLines />
 <tickMarks display="true" />
 </axisGrid>
 <axisLabel />
 <markers />
 <plotEquations>
 <plotEquation>
 <math>
 <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">u</id>
 </math>
 <math>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 </plotEquations>
 <xyDomain scale-type="linear" auto-scale="true">
 <startValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </startValue>
 <secondTickValue resultRef="52">
 <real xmlns="http://schemas.mathsoft.com/math50">0.9</real>
 </secondTickValue>
 <endValue resultRef="53">
 <real xmlns="http://schemas.mathsoft.com/math50">9</real>
 </endValue>
 </xyDomain>
 </xAxis>
 <yAxis rank="1" legend-position="PlotBoundaryLeft" start="0" end="12">
 <axisLine position="origin" positionticmark="0" legendWidth="126.556666666667" />
 <axisGrid>
 <gridFrequency>13</gridFrequency>
 <gridLabels display="true" />
 <gridLines />
 <tickMarks display="true" />
 </axisGrid>
 <axisLabel />
 <markers />
 <plotEquations>
 <plotEquation>
 <math>
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <indexer />
 <id xml:space="preserve">
 I<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">int</Subscript>
 </id>
 <id xml:space="preserve">u</id>
 </apply>
 </math>
 <math>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 <plotEquation>
 <math>
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <plus />
 <apply>
 <indexer />
 <id xml:space="preserve">
 I<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">int</Subscript>
 </id>
 <id xml:space="preserve">u</id>
 </apply>
 <apply>
 <indexer />
 <id xml:space="preserve">
 E<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">int</Subscript>
 </id>
 <id xml:space="preserve">u</id>
 </apply>
 </apply>
 </math>
 <math>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 <plotEquation>
 <math>
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <minus />
 <apply>
 <indexer />
 <id xml:space="preserve">
 I<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">int</Subscript>
 </id>
 <id xml:space="preserve">u</id>
 </apply>
 <apply>
 <indexer />
 <id xml:space="preserve">
 E<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">int</Subscript>
 </id>
 <id xml:space="preserve">u</id>
 </apply>
 </apply>
 </math>
 <math>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 </plotEquations>
 <xyDomain scale-type="linear" auto-scale="true">
 <startValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </startValue>
 <endValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </endValue>
 </xyDomain>
 </yAxis>
 </axes>
 </xyPlot>
 </plot>
</region>

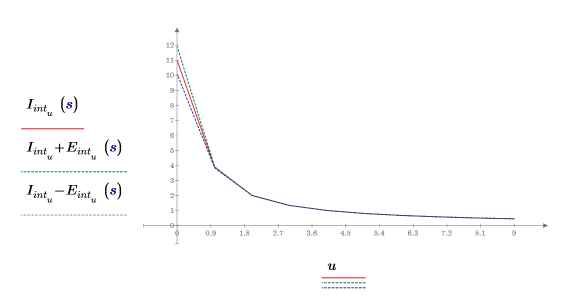
Der Fehler ist zunächst relativ groß und ist nach dem zweiten Interpolationspunkt zu vernachlässigen.

Polynomische Iteration

1. Verwenden Sie die Funktion polyiter, um die Iterationsfunktion am Wert der angegebenen unabhängigen Variable, die Anzahl maximaler Iterationen und die Toleranz auszuwerten.

<region id="ID0EBUMU" actualWidth="261.85" actualHeight="62.800000000000004" top="1900.8000000000002" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
 <math resultRef="54">
 <eval xmlns="http://schemas.mathsoft.com/math50">
 <apply>
 <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">polyiter</id>
 <sequence>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">X</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">Y</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">U</id>
 <real>2</real>
 <apply>
 <scale />
 <real>0.1</real>
 <id labels="UNIT" xml:space="preserve" label-is-contextual="true">s</id>
 </apply>
 </sequence>
 </apply>
 <unitOverride>
 <placeholder />
 </unitOverride>
 </eval>
 <resultFormat>
 <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
 </resultFormat>
 </math>
</region>

<region id="ID0EPUMU" actualWidth="261.85" actualHeight="62.800000000000004" top="1977.6000000000004" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
 <math resultRef="55">
 <eval xmlns="http://schemas.mathsoft.com/math50">
 <apply>
 <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">polyiter</id>
 <sequence>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">X</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">Y</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">U</id>
 <real>5</real>
 <apply>
 <scale />
 <real>0.1</real>
 <id labels="UNIT" xml:space="preserve" label-is-contextual="true">s</id>
 </apply>
 </sequence>
 </apply>
 <unitOverride>
 <placeholder />
 </unitOverride>
 </eval>
 <resultFormat>
 <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
 </resultFormat>
 </math>
</region>

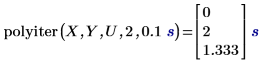
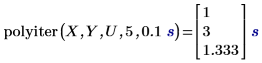
• Der Algorithmus hält an, wenn die letzten beiden iterierten Schätzungen des Datenpunkts innerhalb des Toleranzwerts liegen oder wenn die Anzahl der Iterationen die maximal zulässige Anzahl erreicht.

• Das erste Ergebnis zeigt, dass die Iterationsfunktion nach dem Erreichen der maximalen zulässigen Anzahl von zwei Iterationen nicht konvergieren konnte; daher gab sie das entsprechende Element im Vektor Y zurück.

• Das zweite Ergebnis zeigt, dass die Iterationsfunktion nach der dritten Iteration konvergierte und die maximal zulässige Anzahl von fünf Iterationen nicht erreicht wurde.

2. Werten Sie die Iterationsfunktion mit einem kurzen Programm an zehn unterschiedlichen Punkten aus. Verwenden Sie das Funktionsaugment, um den Fehlerwert in der vierten Spalte der zurückgegebenen Matrix hinzuzufügen, die den Zusammenführungsstatus in der ersten Spalte, die Anzahl verwendeter Iterationen in der zweiten Spalte und die iterierten Werte in der dritten Spalte anzeigt.

<region id="ID0ED1MU" actualWidth="487.13666666666654" actualHeight="200.2" top="2284.8" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
 <math resultRef="56">
 <define xmlns="http://schemas.mathsoft.com/math50">
 <function>
 <id labels="VARIABLE" xml:space="preserve">
 P<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">itr</Subscript>
 </id>
 <boundVars>
 <id labels="VARIABLE" xml:space="preserve">ord</id>
 <id labels="VARIABLE" xml:space="preserve">err</id>
 </boundVars>
 </function>
 <program>
 <localDefine>
 <id labels="VARIABLE" xml:space="preserve">order</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">ord</id>
 </localDefine>
 <localDefine>
 <id labels="VARIABLE" xml:space="preserve">error</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">err</id>
 </localDefine>
 <for>
 <id labels="VARIABLE" xml:space="preserve">u</id>
 <range>
 <real>0</real>
 <apply>
 <minus />
 <apply>
 <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">length</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">X</id>
 </apply>
 <real>1</real>
 </apply>
 </range>
 <program>
 <localDefine>
 <apply>
 <indexer />
 <id labels="VARIABLE" xml:space="preserve">K</id>
 <id labels="*" xml:space="preserve">u</id>
 </apply>
 <apply>
 <mult />
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">error</id>
 <id labels="UNIT" xml:space="preserve" label-is-contextual="true">s</id>
 </apply>
 </localDefine>
 <for>
 <id labels="VARIABLE" xml:space="preserve">v</id>
 <range>
 <real>0</real>
 <real>2</real>
 </range>
 <program>
 <localDefine>
 <apply>
 <indexer />
 <id labels="VARIABLE" xml:space="preserve">N</id>
 <sequence>
 <id labels="*" xml:space="preserve">u</id>
 <id labels="*" xml:space="preserve">v</id>
 </sequence>
 </apply>
 <apply>
 <indexer />
 <parens>
 <apply>
 <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">polyiter</id>
 <sequence>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">X</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">Y</id>
 <apply>
 <mult />
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">u</id>
 <id labels="UNIT" xml:space="preserve">m</id>
 </apply>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">order</id>
 <apply>
 <scale />
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">error</id>
 <id labels="UNIT" xml:space="preserve">s</id>
 </apply>
 </sequence>
 </apply>
 </parens>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">v</id>
 </apply>
 </localDefine>
 </program>
 </for>
 </program>
 </for>
 <localDefine>
 <id labels="VARIABLE" xml:space="preserve">Z</id>
 <apply>
 <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">augment</id>
 <sequence>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">N</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">K</id>
 </sequence>
 </apply>
 </localDefine>
 <return>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">Z</id>
 </return>
 </program>
 </define>
 <resultFormat>
 <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
 </resultFormat>
 </math>
</region>

3. Speichern Sie die Interpolationspunkte und die Fehlerwerte in unabhängigen Vektoren.

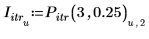
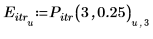
4. Plotten Sie die Iterationspunkte für drei Iterationen und einen Fehler von 0.25.

<region id="ID0ER4MU" actualWidth="577" actualHeight="307.20000000000005" top="2707.2000000000003" left="38.400000000000006" height="307.20000000000005" width="577" xmlns="http://schemas.mathsoft.com/worksheet50">
 <plot background-type="white" origin-positioning="true">
 <xyPlot>
 <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
 <legend />
 <traces>
 <trace resultRef="59">
 <traceStyle color="#FFED1D2F" symbol="filledRectangle" line-weight="1" line-style="Solid">Linien</traceStyle>
 </trace>
 <trace resultRef="60">
 <traceStyle color="#FF008000" symbol="none" line-weight="1" line-style="Dash">Linien</traceStyle>
 </trace>
 <trace resultRef="61">
 <traceStyle color="#FF0000FF" symbol="none" line-weight="1" line-style="Dash">lines</traceStyle>
 </trace>
 </traces>
 <graph-size width="419.4" height="230.4" />
 <axes>
 <xAxis rank="1" legend-position="PlotBoundaryBottom" start="0" end="9">
 <axisLine position="bottom" positionticmark="-1" legendWidth="61.21" />
 <axisGrid>
 <gridFrequency>10</gridFrequency>
 <gridLabels display="true" />
 <gridLines />
 <tickMarks display="true" />
 </axisGrid>
 <axisLabel />
 <markers />
 <plotEquations>
 <plotEquation>
 <math>
 <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">u</id>
 </math>
 <math>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 </plotEquations>
 <xyDomain scale-type="linear" auto-scale="true">
 <startValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </startValue>
 <secondTickValue resultRef="62">
 <real xmlns="http://schemas.mathsoft.com/math50">1</real>
 </secondTickValue>
 <endValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </endValue>
 </xyDomain>
 </xAxis>
 <yAxis rank="1" legend-position="PlotBoundaryLeft" start="0.25" end="3.55">
 <axisLine position="origin" positionticmark="0" legendWidth="123.37" />
 <axisGrid>
 <gridFrequency>12</gridFrequency>
 <gridLabels display="true" />
 <gridLines />
 <tickMarks display="true" />
 </axisGrid>
 <axisLabel />
 <markers />
 <plotEquations>
 <plotEquation>
 <math>
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <indexer />
 <id xml:space="preserve">
 I<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">itr</Subscript>
 </id>
 <id xml:space="preserve">u</id>
 </apply>
 </math>
 <math>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 <plotEquation>
 <math>
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <plus />
 <apply>
 <indexer />
 <id xml:space="preserve">
 I<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">itr</Subscript>
 </id>
 <id xml:space="preserve">u</id>
 </apply>
 <apply>
 <indexer />
 <id xml:space="preserve">
 E<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">itr</Subscript>
 </id>
 <id xml:space="preserve">u</id>
 </apply>
 </apply>
 </math>
 <math>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 <plotEquation>
 <math>
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <minus />
 <apply>
 <indexer />
 <id xml:space="preserve">
 I<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">itr</Subscript>
 </id>
 <id xml:space="preserve">u</id>
 </apply>
 <apply>
 <indexer />
 <id xml:space="preserve">
 E<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">itr</Subscript>
 </id>
 <id xml:space="preserve">u</id>
 </apply>
 </apply>
 </math>
 <math>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 </plotEquations>
 <xyDomain scale-type="linear" auto-scale="true">
 <startValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </startValue>
 <endValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </endValue>
 </xyDomain>
 </yAxis>
 </axes>
 </xyPlot>
 </plot>
</region>

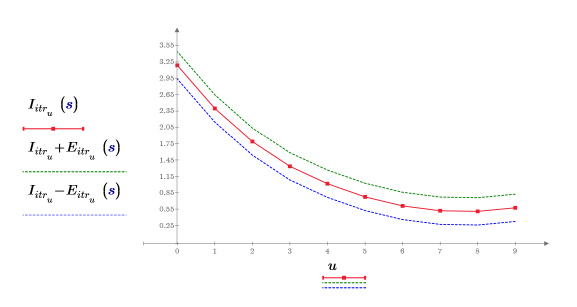
Der Fehler ist an jedem Interpolationspunkt konstant.

5. Vergleichen Sie die zurückgegebenen Ergebnisse der Interpolation und Iteration, wenn die maximale Anzahl der Iterationen auf 3 und der Fehler auf 0.25 festgelegt wird.

<region id="ID0EF6MU" actualWidth="576.60000000000014" actualHeight="287.99999999999994" top="3129.6000000000004" left="38.400000000000006" height="287.99999999999994" width="576.60000000000014" xmlns="http://schemas.mathsoft.com/worksheet50">
 <plot background-type="white" origin-positioning="true">
 <xyPlot>
 <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
 <legend />
 <traces>
 <trace resultRef="63">
 <traceStyle color="#FFED1D2F" symbol="none" line-weight="1" line-style="Solid">Linien</traceStyle>
 </trace>
 <trace resultRef="64">
 <traceStyle color="#FF068149" symbol="filledRectangle" line-weight="2" line-style="DashDotDot">lines</traceStyle>
 </trace>
 </traces>
 <graph-size width="457.4" height="230.4" />
 <axes>
 <xAxis rank="1" legend-position="PlotBoundaryBottom" start="0" end="9">
 <axisLine position="origin" positionticmark="0" legendWidth="61.21" />
 <axisGrid>
 <gridFrequency>11</gridFrequency>
 <gridLabels display="true" />
 <gridLines />
 <tickMarks display="true" />
 </axisGrid>
 <axisLabel />
 <markers />
 <plotEquations>
 <plotEquation>
 <math>
 <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">u</id>
 </math>
 <math>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 </plotEquations>
 <xyDomain scale-type="linear" auto-scale="true">
 <startValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </startValue>
 <endValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </endValue>
 </xyDomain>
 </xAxis>
 <yAxis rank="1" legend-position="PlotBoundaryLeft" start="0" end="12">
 <axisLine position="origin" positionticmark="0" legendWidth="81.1466666666667" />
 <axisGrid>
 <gridFrequency>13</gridFrequency>
 <gridLabels display="true" />
 <gridLines />
 <tickMarks display="true" />
 </axisGrid>
 <axisLabel />
 <markers />
 <plotEquations>
 <plotEquation>
 <math>
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <indexer />
 <id xml:space="preserve">
 I<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">int</Subscript>
 </id>
 <id xml:space="preserve">u</id>
 </apply>
 </math>
 <math>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 <plotEquation>
 <math>
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <indexer />
 <id xml:space="preserve">
 I<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">itr</Subscript>
 </id>
 <id xml:space="preserve">u</id>
 </apply>
 </math>
 <math>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 </plotEquations>
 <xyDomain scale-type="linear" auto-scale="true">
 <startValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </startValue>
 <endValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </endValue>
 </xyDomain>
 </yAxis>
 </axes>
 </xyPlot>
 </plot>
</region>

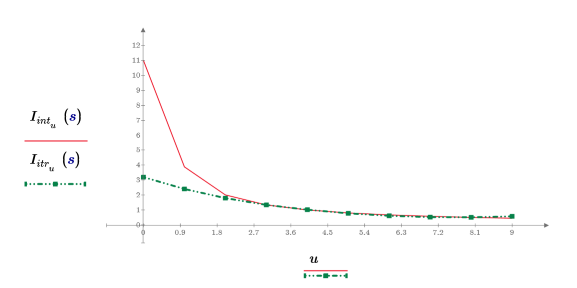
6. Zeigen Sie, dass das Ergebnis der Interpolation mit dem Ergebnis der Iteration identisch ist, wenn die Anzahl von Iterationen auf eine große Zahl und der Fehler auf null festgelegt wird.

<region id="ID0EDBNU" actualWidth="576.6" actualHeight="288" top="3571.2000000000007" left="38.400000000000006" height="288" width="576.6" xmlns="http://schemas.mathsoft.com/worksheet50">
 <plot background-type="white" origin-positioning="true">
 <xyPlot>
 <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
 <legend />
 <traces>
 <trace resultRef="66">
 <traceStyle color="#FFED1D2F" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
 </trace>
 <trace resultRef="67">
 <traceStyle color="#FF068149" symbol="filledRectangle" line-weight="2" line-style="DashDotDot">lines</traceStyle>
 </trace>
 </traces>
 <graph-size width="457.4" height="230.4" />
 <axes>
 <xAxis rank="1" legend-position="PlotBoundaryBottom" start="0" end="9">
 <axisLine position="origin" positionticmark="0" legendWidth="61.21" />
 <axisGrid>
 <gridFrequency>11</gridFrequency>
 <gridLabels display="true" />
 <gridLines />
 <tickMarks display="true" />
 </axisGrid>
 <axisLabel />
 <markers />
 <plotEquations>
 <plotEquation>
 <math>
 <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">u</id>
 </math>
 <math>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 </plotEquations>
 <xyDomain scale-type="linear" auto-scale="true">
 <startValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </startValue>
 <endValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </endValue>
 </xyDomain>
 </xAxis>
 <yAxis rank="1" legend-position="PlotBoundaryLeft" start="0" end="12">
 <axisLine position="origin" positionticmark="0" legendWidth="87.5333333333333" />
 <axisGrid>
 <gridFrequency>13</gridFrequency>
 <gridLabels display="true" />
 <gridLines />
 <tickMarks display="true" />
 </axisGrid>
 <axisLabel />
 <markers />
 <plotEquations>
 <plotEquation>
 <math>
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <indexer />
 <id xml:space="preserve">
 I<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">int</Subscript>
 </id>
 <id xml:space="preserve">u</id>
 </apply>
 </math>
 <math>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 <plotEquation>
 <math>
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <indexer />
 <id xml:space="preserve">
 I0<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">itr</Subscript>
 </id>
 <id xml:space="preserve">u</id>
 </apply>
 </math>
 <math>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 </plotEquations>
 <xyDomain scale-type="linear" auto-scale="true">
 <startValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </startValue>
 <endValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </endValue>
 </xyDomain>
 </yAxis>
 </axes>
 </xyPlot>
 </plot>
</region>

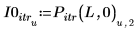
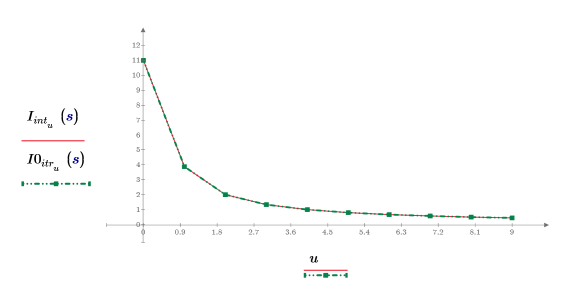
Die maximale Anzahl der Iterationen muss kleiner sein als die Länge der Eingabevektoren.

Zugehörige Themen

Polynominterpolation

War dies hilfreich?