Beispiel: Grenzwertoperator verwenden
Unendlichkeit als Grenzwert verwenden
1. Verwenden Sie den Grenzwertoperator, und werten Sie symbolisch einen Ausdruck aus, wenn sein Argument in Richtung Unendlichkeit verläuft.
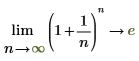
2. Plotten Sie die Funktion, um die Visualisierung zu erleichtern. Verwenden Sie einen horizontalen Markierer, um e darzustellen.
 |  |  |
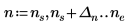 | ||
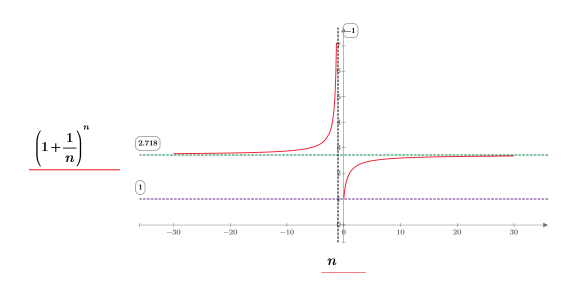 | ||
Im Quadranten (x, y) beobachten wir Folgendes:
◦ Wenn n sich an positive infinity annähert, nähert sich die Funktion an y=e an.
◦ Wenn n sich an 0 annähert, nähert sich die Funktion an y=1 an.
Mathematisch wird dies durch die folgenden symbolischen Auswertungen dargestellt:
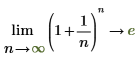 | 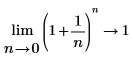 |
Im Quadranten (-x, y) beobachten wir Folgendes:
◦ Wenn n sich an negative infinity annähert, nähert sich die Funktion an y=e an.
◦ Wenn n sich an -1 annähert, nähert sich die Funktion an y=infinity an.
Mathematisch wird dies durch die folgenden symbolischen Auswertungen dargestellt:
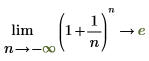 | 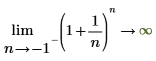 |
Die Verwendung der linken Grenzwertseite in der zweiten Gleichung bedeutet, dass sich -1 von der linken Seite der Kurve her angenähert werden muss. Wenn dies nicht angegeben ist, gibt die Auswertung "nicht definiert" zurück, da die Funktion für -1 < n < 0 nicht definiert ist: 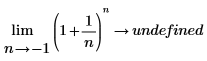 |
Grenzwertseite verwenden
1. Stellen Sie die Funktion cot grafisch dar.
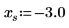 | 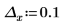 | 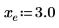 |
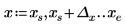 | ||
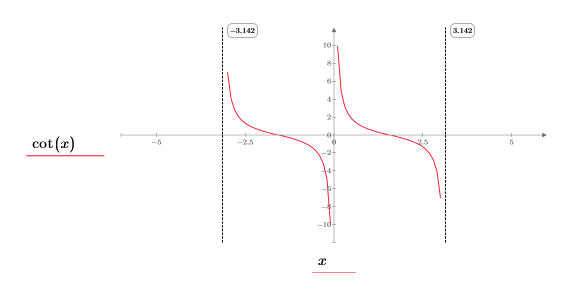 | ||
Im Quadranten (x, y) beobachten wir Folgendes:
◦ Wenn x sich an 0 annähert, nähert sich die Funktion an y=infinity an.
◦ Wenn x sich an π annähert, nähert sich die Funktion an y=-infinity an.
Mathematisch wird dies durch die folgenden symbolischen Auswertungen dargestellt:
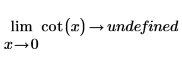 | 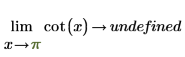 |
Da die Funktion rings um x=+/- n*π/2 symmetrisch ist, gibt die symbolische Auswertung "nicht definiert" zurück, weil die Funktion um x=0 (und alle Mehrfachen von π) entweder infinity oder -infinity lauten kann, abhängig von der Seite, von der aus sich x an 0 annähert.
Dies ist ein guter Fall zum Angeben der "Grenzwertseite".
2. Geben Sie die "Grenzwertseite" an, und werten Sie die Funktion cot um 0 und π erneut symbolisch aus.
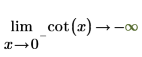 | 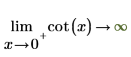 |
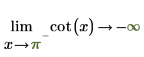 | 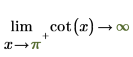 |
Die zurückgegebenen Ergebnisse stimmen mit dem Diagramm überein.
Manchmal hilft es, eine Funktion zu plotten, um sie zu visualisieren und die Gültigkeit von Ergebnissen der symbolischen Auswertung nochmals zu prüfen. |