Beispiel: Vergleichsoption mit den Suchfunktionen verwenden

Funktionen > Vektor und Matrix > Weitere Array-Funktionen > Beispiel: Vergleichsoption mit den Suchfunktionen verwenden

1. Definieren Sie zwei Eingabematrizen A und B mit den gleichen Dimensionen.

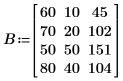2. Legen Sie die Variable z fest.

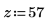
3. Verwenden Sie die Funktion match, um die Elemente in der Matrix A zu finden, die genau mit z übereinstimmen.

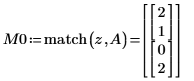
Die Funktion gibt die Zeilen-Spalten-Koordinaten der beiden Elemente der Matrix A zurück, die dem Suchkriterium entsprechen.

4. Schreiben Sie ein Programm, um die von der Funktion match gefundenen Elemente anzuzeigen.

<region id="ID0E61IGB" actualWidth="247.09000000000003" actualHeight="258.4" top="460.80000000000007" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
 <math resultRef="101">
 <define xmlns="http://schemas.mathsoft.com/math50">
 <function>
 <id labels="VARIABLE" xml:space="preserve">F</id>
 <boundVars>
 <id labels="VARIABLE" xml:space="preserve">z</id>
 <id labels="VARIABLE" xml:space="preserve">f</id>
 </boundVars>
 </function>
 <program>
 <if>
 <test>
 <apply>
 <equal />
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">f</id>
 <real>0</real>
 </apply>
 </test>
 <then>
 <program>
 <localDefine>
 <id labels="VARIABLE" xml:space="preserve">M</id>
 <apply>
 <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">match</id>
 <sequence>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">z</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">A</id>
 </sequence>
 </apply>
 </localDefine>
 </program>
 </then>
 <else>
 <program>
 <localDefine>
 <id labels="VARIABLE" xml:space="preserve">M</id>
 <apply>
 <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">match</id>
 <sequence>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">z</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">A</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">f</id>
 </sequence>
 </apply>
 </localDefine>
 </program>
 </else>
 </if>
 <for>
 <id labels="VARIABLE" xml:space="preserve">p</id>
 <range>
 <real>0</real>
 <apply>
 <minus />
 <apply>
 <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">rows</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">M</id>
 </apply>
 <real>1</real>
 </apply>
 </range>
 <program>
 <localDefine>
 <id labels="VARIABLE" xml:space="preserve">r</id>
 <apply>
 <indexer />
 <parens>
 <apply>
 <indexer />
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">M</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">p</id>
 </apply>
 </parens>
 <real>0</real>
 </apply>
 </localDefine>
 <localDefine>
 <id labels="VARIABLE" xml:space="preserve">c</id>
 <apply>
 <indexer />
 <parens>
 <apply>
 <indexer />
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">M</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">p</id>
 </apply>
 </parens>
 <real>1</real>
 </apply>
 </localDefine>
 <localDefine>
 <apply>
 <indexer />
 <id labels="VARIABLE" xml:space="preserve">Q</id>
 <id labels="*" xml:space="preserve">p</id>
 </apply>
 <apply>
 <indexer />
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">A</id>
 <sequence>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">r</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">c</id>
 </sequence>
 </apply>
 </localDefine>
 </program>
 </for>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">Q</id>
 </program>
 </define>
 <resultFormat>
 <matrix size="12,1" offset="1,0" show-indices="false" expand-nested-arrays="false" />
 </resultFormat>
 </math>
</region>

5. Verwenden Sie das Programm, um die genau mit dem Suchkriterium übereinstimmenden Elemente anzuzeigen, wenn z=57.

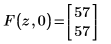
6. Verwenden Sie die Funktion lookup, um Elemente in der Matrix B zu suchen, die mit den in der Matrix A gefundenen Elementen übereinstimmen.

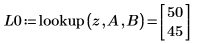
Die Funktion gibt die übereinstimmenden Elemente und nicht ihre Zeilen-Spalten-Koordinaten zurück.

7. Schreiben Sie ein Programm, um die von der Funktion lookup gefundenen Elemente anzuzeigen.

<region id="ID0EVAJGB" actualWidth="267.36666666666673" actualHeight="102.4" top="1017.6000000000001" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
 <math resultRef="107">
 <define xmlns="http://schemas.mathsoft.com/math50">
 <function>
 <id labels="VARIABLE" xml:space="preserve">L</id>
 <boundVars>
 <id labels="VARIABLE" xml:space="preserve">z</id>
 <id labels="VARIABLE" xml:space="preserve">f</id>
 </boundVars>
 </function>
 <program>
 <if>
 <test>
 <apply>
 <equal />
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">f</id>
 <real>0</real>
 </apply>
 </test>
 <then>
 <program>
 <localDefine>
 <id labels="VARIABLE" xml:space="preserve">M</id>
 <apply>
 <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">lookup</id>
 <sequence>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">z</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">A</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">B</id>
 </sequence>
 </apply>
 </localDefine>
 </program>
 </then>
 <else>
 <program>
 <localDefine>
 <id labels="VARIABLE" xml:space="preserve">M</id>
 <apply>
 <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">lookup</id>
 <sequence>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">z</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">A</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">B</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">f</id>
 </sequence>
 </apply>
 </localDefine>
 </program>
 </else>
 </if>
 </program>
 </define>
 </math>
</region>

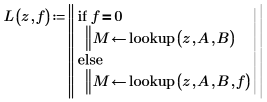
8. Verwenden Sie das Programm, um die übereinstimmenden Elemente der Matrix B anzuzeigen, wenn z=57.

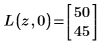
9. Verwenden Sie die beiden Programme, um die Elemente anzuzeigen, die von den Funktionen match und lookup mit der Vergleichsfunktion f1 gefunden werden.

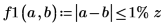
Mit dieser Vergleichsoption werden Werte der Elemente von Matrix A, die innerhalb des Bereichs r1 liegen, gefunden:

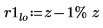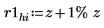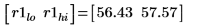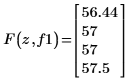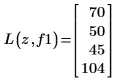10. Verwenden Sie die beiden Programme, um die Elemente anzuzeigen, die von den Funktionen match und lookup mit der Vergleichsfunktion f2 gefunden werden.

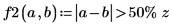
Mit dieser Vergleichsoption werden Werte der Elemente von Matrix A, die außerhalb des Bereichs r2 liegen, gefunden:

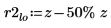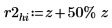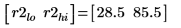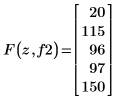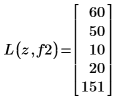11. Schreiben Sie ein Programm, um eine Matrix in einen Vektor zu konvertieren.

<region id="ID0EDRJGB" actualWidth="279.74666666666667" actualHeight="165.152" top="1977.6000000000004" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
 <math resultRef="135">
 <define xmlns="http://schemas.mathsoft.com/math50">
 <function>
 <id labels="VARIABLE" xml:space="preserve">S</id>
 <boundVars>
 <id labels="VARIABLE" xml:space="preserve">M</id>
 </boundVars>
 </function>
 <program>
 <localDefine>
 <apply>
 <indexer />
 <id labels="VARIABLE" xml:space="preserve">T</id>
 <real>0</real>
 </apply>
 <real>0</real>
 </localDefine>
 <for>
 <id labels="VARIABLE" xml:space="preserve">c</id>
 <range>
 <real>0</real>
 <apply>
 <minus />
 <apply>
 <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">cols</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">M</id>
 </apply>
 <real>1</real>
 </apply>
 </range>
 <program>
 <localDefine>
 <id labels="VARIABLE" xml:space="preserve">T</id>
 <apply>
 <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">stack</id>
 <sequence>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">T</id>
 <apply>
 <matcol />
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">M</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">c</id>
 </apply>
 </sequence>
 </apply>
 </localDefine>
 </program>
 </for>
 <for>
 <id labels="VARIABLE" xml:space="preserve">d</id>
 <range>
 <real>1</real>
 <apply>
 <mult />
 <apply>
 <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">rows</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">M</id>
 </apply>
 <apply>
 <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">cols</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">M</id>
 </apply>
 </apply>
 </range>
 <program>
 <localDefine>
 <apply>
 <indexer />
 <id labels="VARIABLE" xml:space="preserve">S</id>
 <apply>
 <minus />
 <id labels="*" xml:space="preserve">d</id>
 <real>1</real>
 </apply>
 </apply>
 <apply>
 <indexer />
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">T</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">d</id>
 </apply>
 </localDefine>
 </program>
 </for>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">S</id>
 </program>
 </define>
 <resultFormat>
 <matrix size="13,1" offset="5,0" show-indices="false" expand-nested-arrays="false" />
 </resultFormat>
 </math>
</region>

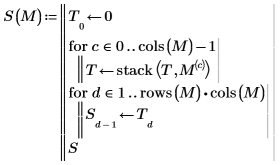
12. Verwenden Sie das Programm, um Matrix A in den Vektor V zu konvertieren.

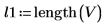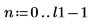13. Ermitteln Sie die Länge des Vektors von Punkten, die in der Matrix A gefunden werden.

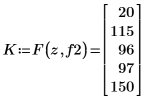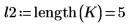14. Schreiben Sie ein Programm, um die gefundenen Punkte in einen neuen Vektor mit der gleichen Länge wie V einzufügen. Das Programm schreibt -100 in leere Positionen.

15. Plotten Sie die beiden Vektoren so, dass die -100-Punkte von MV verborgen sind. Verwenden Sie horizontale Markierungen, um die beiden Ebenen von r2 anzuzeigen.

<region id="ID0EE3JGB" actualWidth="576.8" actualHeight="288" top="3072.0000000000005" left="38.400000000000006" height="288" width="576.8" xmlns="http://schemas.mathsoft.com/worksheet50">
 <plot background-type="white">
 <xyPlot>
 <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
 <legend />
 <traces>
 <trace resultRef="151">
 <traceStyle color="#FF2E3192" symbol="rectangle" line-weight="1" line-style="None">lines</traceStyle>
 </trace>
 <trace resultRef="152">
 <traceStyle color="#FFED1D2F" symbol="circle" line-weight="1" line-style="None">lines</traceStyle>
 </trace>
 </traces>
 <graph-size width="438.4" height="230.4" />
 <axes>
 <xAxis rank="1" legend-position="PlotBoundaryBottom" start="0" end="11">
 <axisLine position="ticknumberlock" positionticmark="1" legendWidth="61.7533333333333" />
 <axisGrid>
 <gridFrequency>12</gridFrequency>
 <gridLabels display="true" />
 <gridLines />
 <tickMarks display="true" />
 </axisGrid>
 <axisLabel />
 <markers />
 <plotEquations>
 <plotEquation>
 <math resultRef="157">
 <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">n</id>
 </math>
 <math resultRef="158">
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 </plotEquations>
 <xyDomain scale-type="linear" auto-scale="true">
 <startValue resultRef="154">
 <real xmlns="http://schemas.mathsoft.com/math50">0</real>
 </startValue>
 <endValue resultRef="156">
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <minus />
 <id xml:space="preserve">l1</id>
 <real>1</real>
 </apply>
 </endValue>
 </xyDomain>
 </xAxis>
 <yAxis rank="1" legend-position="PlotBoundaryLeft" start="-20" end="180">
 <axisLine position="left" positionticmark="-1" legendWidth="96.53" />
 <axisGrid>
 <gridFrequency>11</gridFrequency>
 <gridLabels display="true" />
 <gridLines />
 <tickMarks display="true" />
 </axisGrid>
 <axisLabel />
 <markers>
 <marker resultRef="159" display="true" color="#FFED1D2F" line-style="Dash" value="28.5">
 <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">
 r2<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">lo</Subscript>
 </id>
 </marker>
 <marker resultRef="161" display="true" color="#FFED1D2F" line-style="Dash" value="85.5">
 <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">
 r2<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">hi</Subscript>
 </id>
 </marker>
 </markers>
 <plotEquations>
 <plotEquation>
 <math resultRef="169">
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <indexer />
 <parens>
 <id xml:space="preserve">V</id>
 </parens>
 <id xml:space="preserve">n</id>
 </apply>
 </math>
 <math resultRef="170">
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 <plotEquation>
 <math resultRef="171">
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <indexer />
 <parens>
 <id xml:space="preserve">MV</id>
 </parens>
 <id xml:space="preserve">n</id>
 </apply>
 </math>
 <math resultRef="172">
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 </plotEquations>
 <xyDomain scale-type="linear" auto-scale="true">
 <startValue resultRef="164">
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <neg />
 <id xml:space="preserve">offset</id>
 </apply>
 </startValue>
 <secondTickValue resultRef="166">
 <real xmlns="http://schemas.mathsoft.com/math50">0</real>
 </secondTickValue>
 <endValue resultRef="168">
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <plus />
 <apply>
 <id xml:space="preserve">max</id>
 <id xml:space="preserve">A</id>
 </apply>
 <id xml:space="preserve">offset</id>
 </apply>
 </endValue>
 </xyDomain>
 </yAxis>
 </axes>
 </xyPlot>
 </plot>
</region>

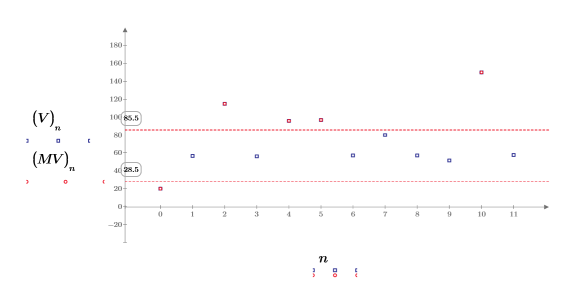
Von den zwölf Elementen des Vektors V (bzw. der Matrix A) befinden sich die fünf gefundenen Elemente außerhalb des angegebenen Bereichs r2.

Zugehörige Themen

Suchfunktionen

War dies hilfreich?