Beispiel: Iteration mit Startwert und Differenzengleichungen
Schätzen Sie Lösungen unter Verwendung von Iterationen mit Startwert.
Quadratwurzeln
Berechnen Sie mit der babylonischen Methode eine Annäherung der Quadratwurzel einer Zahl.
1. Definieren Sie eine positive reelle Zahl X und einen Schätzwert für deren Quadratwurzel.
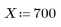
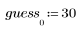
Der erste Schätzwert ist definiert als erstes Element eines Vektors.
2. Definieren Sie N als Anzahl von Iterationen.
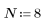
3. Berechnen Sie neue Schätzungen der Quadratwurzel.
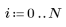
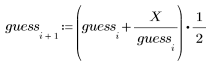
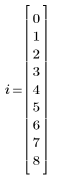 | 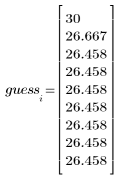 | 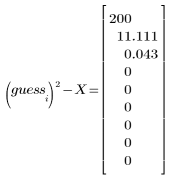 |
Die vordefinierte Quadratwurzelfunktion liefert folgendes Ergebnis:
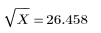
4. Stellen Sie den Vektor von Schätzungen grafisch dar.
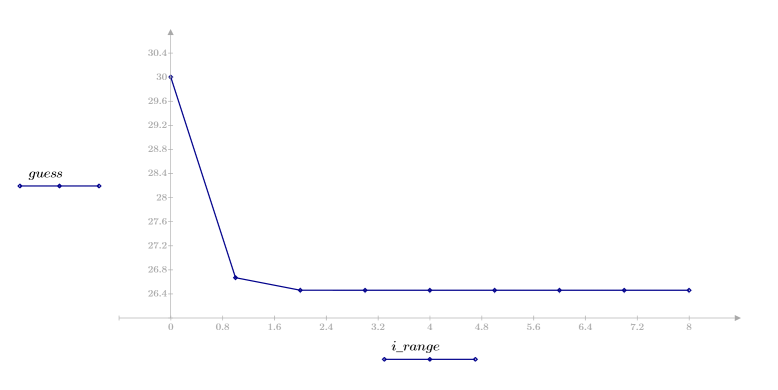
Hier stellt sich die Konvergenz schneller ein. Für andere Fälle können Sie die Anzahl von Iterationen N erhöhen, um den Anforderungen des Problems gerecht zu werden.
Differenzengleichungssysteme
Betrachtet ein Infektionsmodell mit vier Variablen:
• inf – Die Anzahl infizierter Personen
• sus – Die Anzahl anfälliger Personen
• dec – Die Anzahl verstorbener Personen
• rec – Die Anzahl gesundeter Personen
1. Definieren Sie Startwerte für die simultane Iteration.

2. Definieren Sie ein Differenzengleichungssystem.
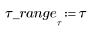
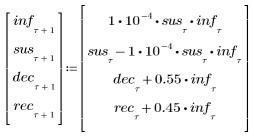
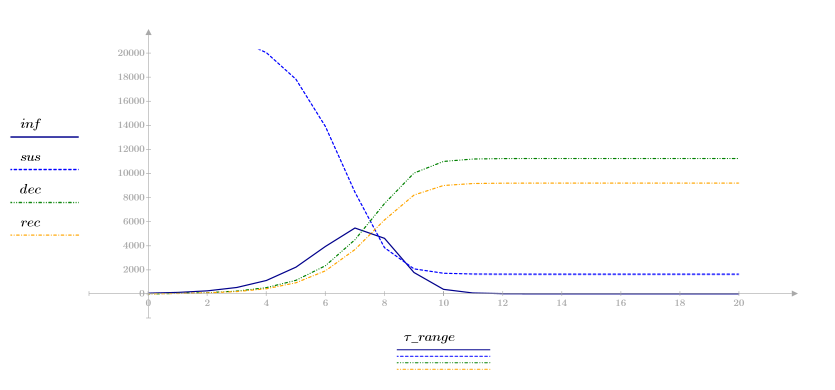
3. Plotten Sie die vier Variablen bezogen auf die Zeit, um zu sehen, wie sich das Infektionsmodell entwickelt.
Matrixdifferenzengleichungen
Betrachten Sie den Markow-Prozess, d.h. eine Vektorzeitfolge, deren gegenwärtiger Zustand durch die Multiplikation des vorherigen Zustandes mit einer Zustandsübergangsmatrix ermittelt wird.
1. Definieren Sie den Anfangszustand des Vektors und die Zustandsübergangsmatrix A.
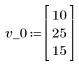

2. Definieren Sie den Iterationsprozess.
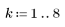
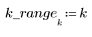
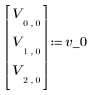
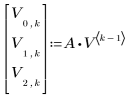
3. Berechnen Sie den Endzustand des Vektors.
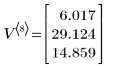
Die Matrix V enthält den Prozessverlauf:
