Beispiel: Quantil-Quantil-Diagramme

Funktionen > Statistik > Grafische Statistik > Beispiel: Quantil-Quantil-Diagramme

Verwenden Sie die Funktion qqplot zum Erstellen von Quantil-Quantil-Diagrammen.

Zwei Datensätze

Vergleichen Sie die Quantile zweier Datensätze in einem Q-Q-Diagramm, um zu prüfen, ob sie die gleiche Verteilung aufweisen.

1. Definieren Sie einen Datensatz.

Spalte 2 enthält die Gruppe, in der die Messung durchgeführt wurde und Spalte 3 enthält die gemessene Stärke von Schiebern aus beschichtetem Siliziumnitrat.

2. Extrahieren Sie die beiden interessierenden Spalten 2 und 3.

<region id="ID0EL1DBB" top="345.6" left="38.400000000000006" height="25.6" width="377.50000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="156">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id labels="*" xml:space="preserve">BatchData</id>
      <apply>
        <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">submatrix</id>
        <sequence>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">Data</id>
          <real>0</real>
          <apply>
            <minus />
            <apply>
              <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">rows</id>
              <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">Data</id>
            </apply>
            <real>1</real>
          </apply>
          <real>2</real>
          <real>3</real>
        </sequence>
      </apply>
    </define>
    <resultFormat>
      <decimal precision="round-trip-decimal-places" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

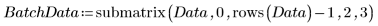
3. Rufen Sie vlookup auf, um die Daten danach zu unterteilen, ob die Messungen in Gruppe 1 oder Gruppe 2 erfolgt sind.

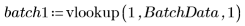
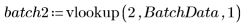
4. Berechnen Sie das erste und dritte Quantil jeder Gruppe.

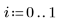
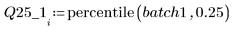
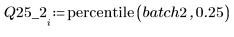
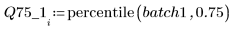
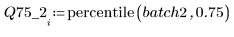
5. Plotten Sie ein Q-Q-Diagramm und die Quantile.

<region id="ID0EIDEBB" top="806.40000000000009" left="19.200000000000003" height="552" width="593.999999999999" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="178">
          <traceStyle color="#FF800080" symbol="x" line-weight="1" line-style="None">lines</traceStyle>
        </trace>
        <trace resultRef="179">
          <traceStyle color="#FF0000FF" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
        <trace resultRef="180">
          <traceStyle color="#FFFF0000" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
        <trace resultRef="181">
          <traceStyle color="#FFFF0000" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
        <trace resultRef="182">
          <traceStyle color="#FF008000" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
        <trace resultRef="183">
          <traceStyle color="#FF008000" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="474.799999999999" height="360" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="345" end="845">
          <axisLine position="bottom" positionticmark="-1" legendWidth="335.533333333333" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="184">
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <matcol />
                  <id xml:space="preserve">qq</id>
                  <real>0</real>
                </apply>
              </math>
              <math resultRef="185">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math resultRef="186">
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">range</id>
              </math>
              <math resultRef="187">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math resultRef="188">
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">Q25_2</id>
              </math>
              <math resultRef="189">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math resultRef="190">
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">Q75_2</id>
              </math>
              <math resultRef="191">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math resultRef="192">
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">range</id>
              </math>
              <math resultRef="193">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="345" end="845">
          <axisLine position="left" positionticmark="-1" legendWidth="95.5333333333333" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="194">
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <matcol />
                  <id xml:space="preserve">qq</id>
                  <real>1</real>
                </apply>
              </math>
              <math resultRef="195">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math resultRef="196">
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">range</id>
              </math>
              <math resultRef="197">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math resultRef="198">
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">range</id>
              </math>
              <math resultRef="199">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math resultRef="200">
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">range</id>
              </math>
              <math resultRef="201">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math resultRef="202">
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">Q25_1</id>
              </math>
              <math resultRef="203">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math resultRef="204">
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">Q75_1</id>
              </math>
              <math resultRef="205">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

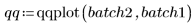
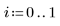
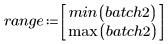
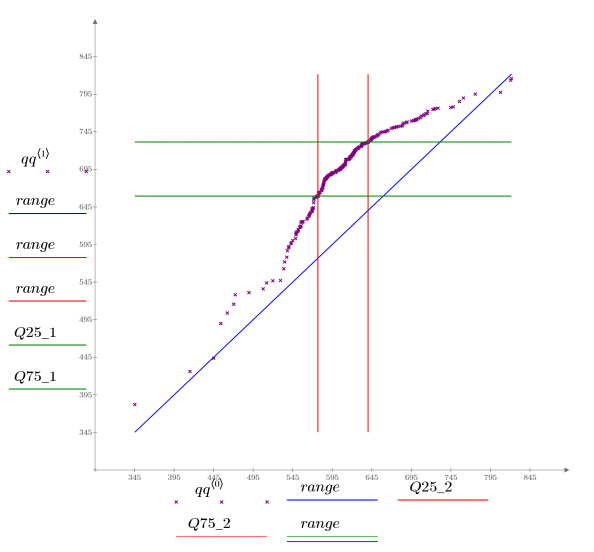
Es wird eine 1:1-Verweislinie geplottet, um die Varianz der Daten hervorzuheben.

Das Q-Q-Diagramm zeigt, dass die beiden Gruppen nicht dieselbe Verteilung haben, obwohl die Werte für sehr kleine und sehr große Perzentile ähnlich sind. Die Perzentile für Gruppe 1 sind deutlich höher als die für Gruppe 2, was auf sehr unterschiedliche Verarbeitungsbedingungen hinweist.

Normalverteilung

Ermitteln Sie, ob die Messungen mit dem Wärmeflussmessgerät zufällig angestellt wurden. Prüfen Sie, ob die Messungen normalverteilt sind, indem Sie sie mit der Normalverteilung in einem Q-Q-Diagramm vergleichen.

1. Definieren Sie einen Datensatz, der den Wärmefluss beschreibt.

2. Ermitteln Sie die Datenpunkte für den Q-Q-Normalplot.

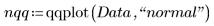
3. Ermitteln Sie die Mittelwertgerade, um festzustellen, wie ähnlich die Datenquantile Quantilen der Normalverteilung sind.

<region id="ID0EDJEBB" top="2016.0000000000002" left="38.400000000000006" height="25.6" width="152.6866666666667" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="234">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <function>
        <id labels="*" xml:space="preserve">BestFit</id>
        <boundVars>
          <id labels="*" xml:space="preserve">x</id>
        </boundVars>
      </function>
      <apply>
        <plus />
        <apply>
          <mult />
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">m</id>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">x</id>
        </apply>
        <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">b</id>
      </apply>
    </define>
    <resultFormat>
      <decimal precision="round-trip-decimal-places" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

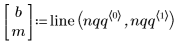
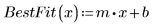
4. Plotten Sie das Q-Q-Diagramm und die Mittelwertgerade.

<region id="ID0EUKEBB" top="2092.8" left="19.200000000000003" height="312" width="590.999999999999" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="236">
          <traceStyle color="#FFFF0000" symbol="x" line-weight="1" line-style="None">lines</traceStyle>
        </trace>
        <trace resultRef="237">
          <traceStyle color="#FF0000FF" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="394.999999999999" height="235.2" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="9.15" end="9.4">
          <axisLine position="origin" positionticmark="5" legendWidth="91.2633333333333" />
          <axisGrid>
            <gridFrequency>6</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="244">
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <matcol />
                  <id xml:space="preserve">nqq</id>
                  <real>0</real>
                </apply>
              </math>
              <math resultRef="245">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="239">
              <real xmlns="http://schemas.mathsoft.com/math50">9.15</real>
            </startValue>
            <secondTickValue resultRef="241">
              <real xmlns="http://schemas.mathsoft.com/math50">9.20</real>
            </secondTickValue>
            <endValue resultRef="243">
              <real xmlns="http://schemas.mathsoft.com/math50">9.35</real>
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="-3.5" end="3.5">
          <axisLine position="left" positionticmark="-1" legendWidth="157.56" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="246">
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <matcol />
                  <id xml:space="preserve">nqq</id>
                  <real>1</real>
                </apply>
              </math>
              <math resultRef="247">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math resultRef="248">
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <id xml:space="preserve">BestFit</id>
                  <apply>
                    <matcol />
                    <id xml:space="preserve">nqq</id>
                    <real>0</real>
                  </apply>
                </apply>
              </math>
              <math resultRef="249">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

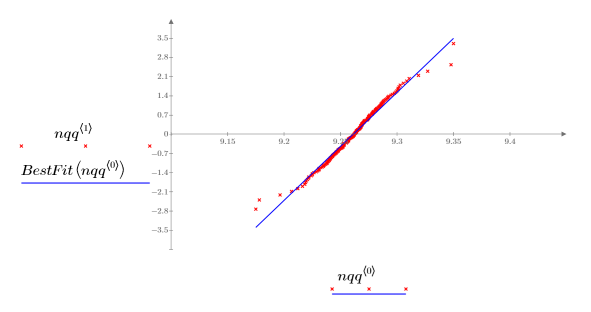
Die sehr enge Korrelation mit der Verweislinie zeigt an, dass die Stichproben normalverteilt sind.

Die Prüfung der Normalität ist einer der Tests, die bei der Ausreißererkennung durchgeführt wird.

Weibull-Verteilung

Testen Sie, ob ein Datensatz einer Weibull-Verteilung entspricht.

1. Verzeichnen Sie im Vektor R die Voltzahl des Stromdurchgangs bei elektrisch isolierten Kabeln, die zunehmender Spannungsbelastung ausgesetzt sind.

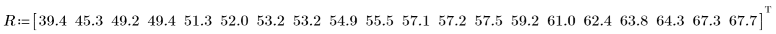
2. Plotten Sie ein Histogramm der Daten.

<region id="ID0EAQEBB" top="2880.0000000000005" left="19.200000000000003" height="312" width="589.906666755675" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="267">
          <traceStyle color="#FFFF0000" symbol="none" line-weight="1" line-style="Solid">columns</traceStyle>
        </trace>
      </traces>
      <graph-size width="470.706666755675" height="254.4" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="32.5" end="72.5">
          <axisLine position="origin" positionticmark="0" legendWidth="115.576666666667" />
          <axisGrid>
            <gridFrequency>9</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="270">
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <plus />
                  <id xml:space="preserve">bins</id>
                  <real>2.5</real>
                </apply>
              </math>
              <math resultRef="271">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <secondTickValue resultRef="269">
              <real xmlns="http://schemas.mathsoft.com/math50">37.5</real>
            </secondTickValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="0" end="5">
          <axisLine position="left" positionticmark="-1" legendWidth="85.6133333333333" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="272">
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">stem</id>
              </math>
              <math resultRef="273">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

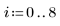
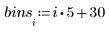
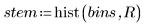
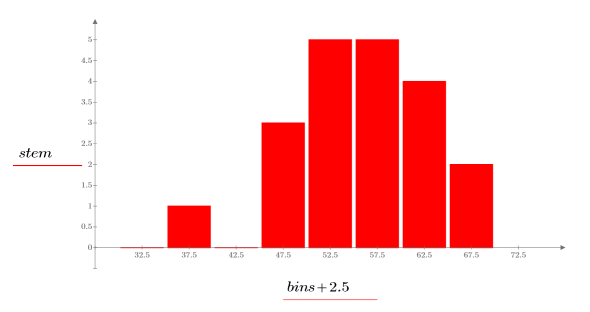
Das Histogramm zeigt, dass die Daten nicht normalverteilt sind. Die Daten sind nach einer Seite hin verzerrt. Sie können die Daten mit einer Weibull-Verteilung in einem Q-Q-Diagramm vergleichen.

3. Ermitteln Sie die Datenpunkte für das Weilbull-Q-Q-Diagramm.

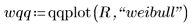
4. Ermitteln Sie die Mittelwertgerade, um zu sehen, wie stark die Datenquantile den Quantilen einer Weibull-Verteilung ähneln.

<region id="ID0EVTEBB" top="3494.4000000000005" left="38.400000000000006" height="25.6" width="152.6866666666667" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="283">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <function>
        <id labels="*" xml:space="preserve">BestFit</id>
        <boundVars>
          <id labels="*" xml:space="preserve">x</id>
        </boundVars>
      </function>
      <apply>
        <plus />
        <apply>
          <mult />
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">m</id>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">x</id>
        </apply>
        <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">b</id>
      </apply>
    </define>
    <resultFormat>
      <decimal precision="round-trip-decimal-places" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

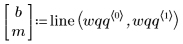
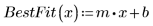
5. Plotten Sie das Q-Q-Diagramm und die Mittelwertgerade.

<region id="ID0EGVEBB" top="3571.2000000000007" left="19.200000000000003" height="312" width="592.999999999999" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="285">
          <traceStyle color="#FFFF0000" symbol="x" line-weight="1" line-style="None">lines</traceStyle>
        </trace>
        <trace resultRef="286">
          <traceStyle color="#FF0000FF" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="396.999999999999" height="235.2" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="3.6" end="4.3">
          <axisLine position="origin" positionticmark="8" legendWidth="93.3466666666667" />
          <axisGrid>
            <gridFrequency>8</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="293">
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <matcol />
                  <id xml:space="preserve">wqq</id>
                  <real>0</real>
                </apply>
              </math>
              <math resultRef="294">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="288">
              <real xmlns="http://schemas.mathsoft.com/math50">3.60</real>
            </startValue>
            <secondTickValue resultRef="290">
              <real xmlns="http://schemas.mathsoft.com/math50">3.7</real>
            </secondTickValue>
            <endValue resultRef="292">
              <real xmlns="http://schemas.mathsoft.com/math50">4.3</real>
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="-6.4" end="2.4">
          <axisLine position="left" positionticmark="-1" legendWidth="159.643333333333" />
          <axisGrid>
            <gridFrequency>12</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="295">
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <matcol />
                  <id xml:space="preserve">wqq</id>
                  <real>1</real>
                </apply>
              </math>
              <math resultRef="296">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math resultRef="297">
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <id xml:space="preserve">BestFit</id>
                  <apply>
                    <matcol />
                    <id xml:space="preserve">wqq</id>
                    <real>0</real>
                  </apply>
                </apply>
              </math>
              <math resultRef="298">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

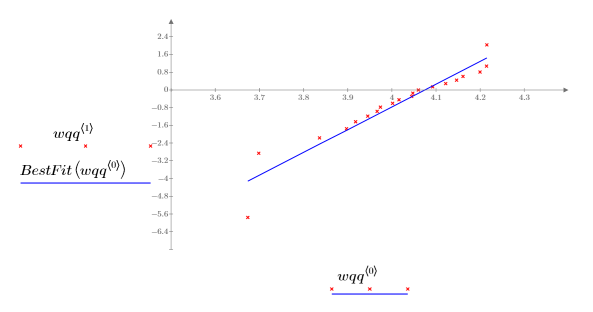
Die starke Korrelation mit der Bezugslinie zeigt an, dass der Datensatz durch eine Weibull-Verteilung modelliert werden kann.

Für Weibull-Q-Q-Diagramme wird ein logarithmischer Maßstab verwendet.

Verweis

Lawless, J.F., Statistical Methods for Lifetime Data, zweite Auflage, Wiley-Interscience, 2002.

Zugehörige Themen

Quantil-Quantil-Diagramm

War dies hilfreich?