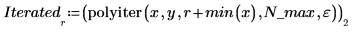Beispiel: Polynominterpolation

Funktionen > Datenanalyse > Interpolation und Vorhersage > Beispiel: Polynominterpolation

polyint

Führen Sie unter Verwendung der Funktion polyint eine Polynominterpolation für einen Datensatz durch.

1. Definieren Sie einen Datensatz.

2. Rufen Sie die Funktion polyint auf, um die Polynominterpolation des Datensatzes an einem bestimmten Punkt zu berechnen.

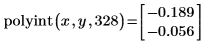
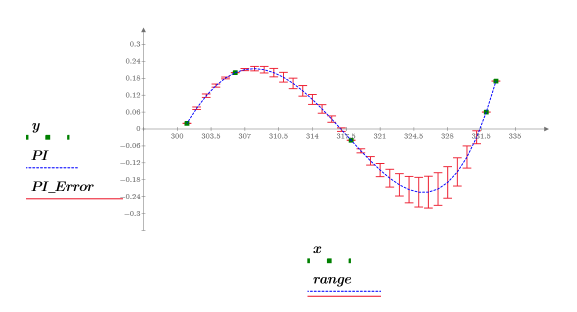
Bei x = 328lautet das interpolierte Ergebnis y = -0.189 mit einem Fehler von 0.056.

3. Definieren Sie den Bereich von x-Werten, für den Sie die interpolierten y-Werte ermitteln möchten.

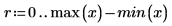
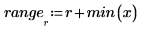
4. Verzeichnen Sie die interpolierten Werte und die zugehörigen Fehler.

<region id="ID0EO6HU" actualWidth="232.55666666666664" actualHeight="36.800000000000004" top="576.00000000000011" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="48">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <indexer />
        <id labels="*" xml:space="preserve">PI</id>
        <id labels="*" xml:space="preserve">r</id>
      </apply>
      <apply>
        <indexer />
        <parens>
          <apply>
            <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">polyint</id>
            <sequence>
              <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">x</id>
              <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">y</id>
              <apply>
                <plus />
                <id xml:space="preserve">r</id>
                <apply>
                  <id xml:space="preserve">min</id>
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">x</id>
                </apply>
              </apply>
            </sequence>
          </apply>
        </parens>
        <real>0</real>
      </apply>
    </define>
    <resultFormat>
      <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

<region id="ID0E36HU" actualWidth="251.71666666666664" actualHeight="36.800000000000004" top="614.40000000000009" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="49">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <indexer />
        <id labels="*" xml:space="preserve">error</id>
        <id labels="*" xml:space="preserve">r</id>
      </apply>
      <apply>
        <indexer />
        <parens>
          <apply>
            <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">polyint</id>
            <sequence>
              <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">x</id>
              <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">y</id>
              <apply>
                <plus />
                <id xml:space="preserve">r</id>
                <apply>
                  <id xml:space="preserve">min</id>
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">x</id>
                </apply>
              </apply>
            </sequence>
          </apply>
        </parens>
        <real>1</real>
      </apply>
    </define>
    <resultFormat>
      <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

<region id="ID0EKAIU" actualWidth="194.07999999999998" actualHeight="36.800000000000004" top="652.80000000000007" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="50">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <indexer />
        <id labels="VARIABLE" xml:space="preserve">PI_Error</id>
        <sequence>
          <id labels="*" xml:space="preserve">r</id>
          <real>0</real>
        </sequence>
      </apply>
      <parens>
        <apply>
          <minus />
          <apply>
            <indexer />
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">PI</id>
            <id xml:space="preserve">r</id>
          </apply>
          <apply>
            <indexer />
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">error</id>
            <id xml:space="preserve">r</id>
          </apply>
        </apply>
      </parens>
    </define>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

<region id="ID0EYAIU" actualWidth="194.07999999999998" actualHeight="36.800000000000004" top="691.2" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="51">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <indexer />
        <id labels="VARIABLE" xml:space="preserve">PI_Error</id>
        <sequence>
          <id labels="*" xml:space="preserve">r</id>
          <real>1</real>
        </sequence>
      </apply>
      <parens>
        <apply>
          <plus />
          <apply>
            <indexer />
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">PI</id>
            <id xml:space="preserve">r</id>
          </apply>
          <apply>
            <indexer />
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">error</id>
            <id xml:space="preserve">r</id>
          </apply>
        </apply>
      </parens>
    </define>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

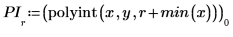
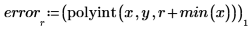
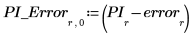
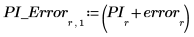
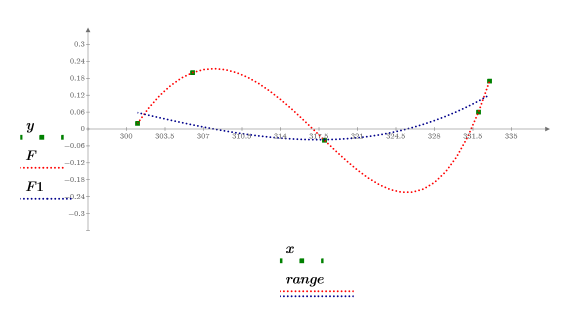
5. Stellen Sie die Datenpunkte, die interpolierte Kurve und die Fehlerschätzung grafisch dar.

<region id="ID0EICIU" actualWidth="577.00000000000023" actualHeight="312" top="902.40000000000009" left="38.400000000000006" height="312" width="577.00000000000023" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="52">
          <traceStyle color="#FF008000" symbol="filledRectangle" line-weight="2" line-style="None">lines</traceStyle>
        </trace>
        <trace resultRef="53">
          <traceStyle color="#FF0000FF" symbol="none" line-weight="1" line-style="Dash">lines</traceStyle>
        </trace>
        <trace resultRef="54">
          <traceStyle color="#FFED1D2F" symbol="none" line-weight="1" line-style="Solid">errors</traceStyle>
        </trace>
      </traces>
      <graph-size width="419.4" height="216" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="300" end="335">
          <axisLine position="ticknumberlock" positionticmark="5" legendWidth="92.1466666666667" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math>
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">x</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">range</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="55">
              <real xmlns="http://schemas.mathsoft.com/math50">300</real>
            </startValue>
            <endValue resultRef="56">
              <real xmlns="http://schemas.mathsoft.com/math50">335</real>
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="-0.3" end="0.3">
          <axisLine position="left" positionticmark="-1" legendWidth="116.403333333333" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math>
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">y</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">PI</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">PI_Error</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="57">
              <real xmlns="http://schemas.mathsoft.com/math50">-0.3</real>
            </startValue>
            <secondTickValue resultRef="58">
              <real xmlns="http://schemas.mathsoft.com/math50">-0.24</real>
            </secondTickValue>
            <endValue resultRef="59">
              <real xmlns="http://schemas.mathsoft.com/math50">0.3</real>
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

polycoeff

Berechnen Sie die interpolierten Werte mit polyint. Verwenden Sie polycoeff, um sowohl das Interpolationspolynom als auch einige seiner Ableitungen zu berechnen. Da die durch polycoeff gegebenen Koeffizienten bei gegebenen Datenpunkten weniger genau sind, stellen sie die interpolierten Werte nicht optimal dar.

1. Ermitteln Sie die Polynomkoeffizienten für die Polynomkurve, die durch den oben definierten Satz an Datenpunkten verläuft.

<region id="ID0ESFIU" actualWidth="139.20333333333332" actualHeight="36.800000000000004" top="1440.0000000000002" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="61">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <indexer />
        <id labels="*" xml:space="preserve">c</id>
        <id labels="*" xml:space="preserve">i</id>
      </apply>
      <apply>
        <indexer />
        <apply>
          <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">polycoeff</id>
          <sequence>
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">x</id>
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">y</id>
          </sequence>
        </apply>
        <id xml:space="preserve">i</id>
      </apply>
    </define>
    <resultFormat>
      <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

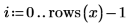
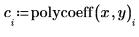
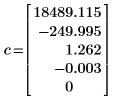
2. Definieren Sie eine Polynomfunktion, wobei c der Vektor von Polynomkoeffizienten ist.

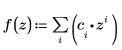
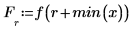
3. Differenzieren Sie die Polynomfunktion.

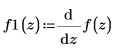
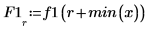
4. Stellen Sie die Datenpunkte, die Polynominterpolation und deren erste Ableitung grafisch dar.

<region id="ID0EQLIU" actualWidth="578" actualHeight="312" top="1900.8000000000002" left="38.400000000000006" height="312" width="578" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="67">
          <traceStyle color="#FF008000" symbol="filledRectangle" line-weight="2" line-style="None">lines</traceStyle>
        </trace>
        <trace resultRef="68">
          <traceStyle color="#FFFF0000" symbol="none" line-weight="2" line-style="Dot">lines</traceStyle>
        </trace>
        <trace resultRef="69">
          <traceStyle color="#FF00008B" symbol="none" line-weight="2" line-style="Dot">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="478" height="216" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="300" end="335">
          <axisLine position="origin" positionticmark="5" legendWidth="92.1466666666667" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math>
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">x</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">range</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="70">
              <real xmlns="http://schemas.mathsoft.com/math50">300</real>
            </startValue>
            <endValue resultRef="71">
              <real xmlns="http://schemas.mathsoft.com/math50">335</real>
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="-0.3" end="0.3">
          <axisLine position="left" positionticmark="-1" legendWidth="70.7" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math>
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">y</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">F</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">F1</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="72">
              <real xmlns="http://schemas.mathsoft.com/math50">-0.3</real>
            </startValue>
            <endValue resultRef="73">
              <real xmlns="http://schemas.mathsoft.com/math50">0.3</real>
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

Die Funktion polycoeff bildet nicht das Polynom der besten Kleinste-Quadrate-Anpassung wie die Funktion polyfit.

Die Ergebnisse von polyint und polycoeff sollten nicht zum Vorhersagen von y-Werten außerhalb des Bereichs der ursprünglichen x-Werte herangezogen werden.

polyiter

Führen Sie mithilfe der Funktion polyiter eine Polynominterpolation durch.

1. Definieren Sie die mögliche maximale Anzahl von Iterationen und die Toleranz.

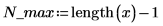
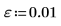
2. Rufen Sie die Funktion polyiter auf.

<region id="ID0EIRIU" actualWidth="294.52333333333331" actualHeight="62.800000000000004" top="2534.4000000000005" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="76">
    <eval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">polyiter</id>
        <sequence>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">x</id>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">y</id>
          <real>328</real>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">N_max</id>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">ε</id>
        </sequence>
      </apply>
      <unitOverride>
        <placeholder />
      </unitOverride>
    </eval>
    <resultFormat>
      <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

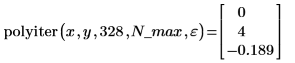
Da der Algorithmus nicht konvergierte, wurde die Berechnung nicht vor der Iteration N_max gestoppt. Er hat keinen Fehler von 0.01 erreicht und dasselbe Ergebnis wie polyint zurückgegeben.

<region id="ID0EDSIU" actualWidth="204.89333333333335" actualHeight="36.800000000000004" top="2668.8" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="77">
    <eval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <indexer />
        <apply>
          <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">polyint</id>
          <sequence>
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">x</id>
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">y</id>
            <real>328</real>
          </sequence>
        </apply>
        <real>0</real>
      </apply>
      <unitOverride>
        <placeholder />
      </unitOverride>
    </eval>
    <resultFormat>
      <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

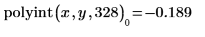
3. Stellen Sie die ursprünglichen Punkte, das exakte Polynom und das iterierte Polynom grafisch dar.

Zugehörige Themen

Lineare Prognose

War dies hilfreich?