Beispiel: Modifizierte Bessel-Funktionen der ersten Art

Funktionen > Spezielle Funktionen > Bessel-Funktionen > Beispiel: Modifizierte Bessel-Funktionen der ersten Art

Zeigen Sie die Beziehung zwischen den Funktionen I0, I1 und In an. Zeigen Sie auch die Beziehungen zwischen diesen Funktionen und ihren skalierten Versionen an.

1. Legen Sie zwei Schrittbereichsvariablen fest:

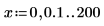
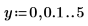
2. Plotten Sie die Funktionen I0 und I1. Fügen Sie dem Diagramm die Funktion In zweiter Ordnung hinzu:

<region id="ID0EX556" actualWidth="591.66857242139008" actualHeight="316.8" top="115.20000000000002" left="0" height="316.8" width="591.66857242139008" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="48">
          <traceStyle color="#FFED1D2F" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
        <trace resultRef="49">
          <traceStyle color="#FF068149" symbol="none" line-weight="1" line-style="Solid">Linien</traceStyle>
        </trace>
        <trace resultRef="50">
          <traceStyle color="#FF2E3192" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="438.06857242139" height="240" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="-1" end="5">
          <axisLine position="origin" positionticmark="0" legendWidth="60.93" />
          <axisGrid>
            <gridFrequency>7</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <plotEquations>
            <plotEquation>
              <math>
                <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true" xmlns="http://schemas.mathsoft.com/math50">x</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="51">
              <real xmlns="http://schemas.mathsoft.com/math50">-1</real>
            </startValue>
            <secondTickValue resultRef="52">
              <real xmlns="http://schemas.mathsoft.com/math50">0</real>
            </secondTickValue>
            <endValue resultRef="53">
              <real xmlns="http://schemas.mathsoft.com/math50">5</real>
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="0" end="10">
          <axisLine position="origin" positionticmark="1" legendWidth="111.28" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <plotEquations>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <id labels="FUNCTION" xml:space="preserve">I0</id>
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">x</id>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <id labels="FUNCTION" xml:space="preserve">I1</id>
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">x</id>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <id labels="FUNCTION" xml:space="preserve">In</id>
                  <sequence>
                    <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">m</id>
                    <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">x</id>
                  </sequence>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="54">
              <real xmlns="http://schemas.mathsoft.com/math50">0</real>
            </startValue>
            <secondTickValue resultRef="55">
              <real xmlns="http://schemas.mathsoft.com/math50">1</real>
            </secondTickValue>
            <endValue resultRef="56">
              <real xmlns="http://schemas.mathsoft.com/math50">10</real>
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

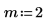
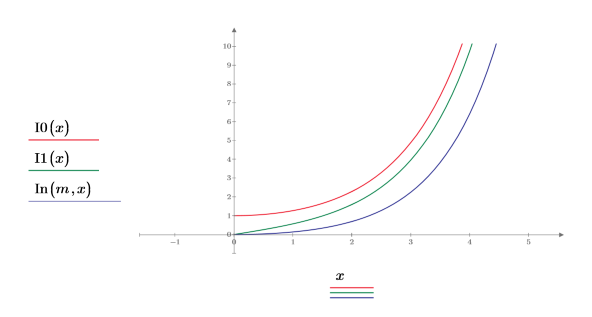
3. Plotten Sie die Funktion In fünfter und achter Ordnung:

<region id="ID0ELA66" actualWidth="590.86857242139" actualHeight="316.8" top="441.60000000000008" left="0" height="316.8" width="590.86857242139" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="57">
          <traceStyle color="#FFED1D2F" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
        <trace resultRef="58">
          <traceStyle color="#FF068149" symbol="none" line-weight="1" line-style="Solid">Linien</traceStyle>
        </trace>
        <trace resultRef="59">
          <traceStyle color="#FF2E3192" symbol="none" line-weight="1" line-style="Solid">Linien</traceStyle>
        </trace>
        <trace resultRef="60">
          <traceStyle color="#FF2E3192" symbol="none" line-weight="1" line-style="Dash">Linien</traceStyle>
        </trace>
        <trace resultRef="61">
          <traceStyle color="#FFCA5053" symbol="none" line-weight="1" line-style="Dash">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="418.06857242139" height="240" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="-1" end="7">
          <axisLine position="origin" positionticmark="0" legendWidth="60.93" />
          <axisGrid>
            <gridFrequency>9</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <plotEquations>
            <plotEquation>
              <math>
                <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true" xmlns="http://schemas.mathsoft.com/math50">x</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="62">
              <real xmlns="http://schemas.mathsoft.com/math50">-1</real>
            </startValue>
            <secondTickValue resultRef="63">
              <real xmlns="http://schemas.mathsoft.com/math50">0</real>
            </secondTickValue>
            <endValue resultRef="64">
              <real xmlns="http://schemas.mathsoft.com/math50">7</real>
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="0" end="2">
          <axisLine position="origin" positionticmark="1" legendWidth="134.01" />
          <axisGrid>
            <gridFrequency>3</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <plotEquations>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <id labels="FUNCTION" xml:space="preserve">I0</id>
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">x</id>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <id labels="FUNCTION" xml:space="preserve">I1</id>
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">x</id>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <id labels="FUNCTION" xml:space="preserve">In</id>
                  <sequence>
                    <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">m</id>
                    <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">x</id>
                  </sequence>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <id labels="FUNCTION" xml:space="preserve">In</id>
                  <sequence>
                    <apply>
                      <plus />
                      <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">m</id>
                      <real>3</real>
                    </apply>
                    <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">x</id>
                  </sequence>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <id labels="FUNCTION" xml:space="preserve">In</id>
                  <sequence>
                    <apply>
                      <plus />
                      <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">m</id>
                      <real>6</real>
                    </apply>
                    <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">x</id>
                  </sequence>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="65">
              <real xmlns="http://schemas.mathsoft.com/math50">0</real>
            </startValue>
            <secondTickValue resultRef="66">
              <real xmlns="http://schemas.mathsoft.com/math50">1</real>
            </secondTickValue>
            <endValue resultRef="67">
              <real xmlns="http://schemas.mathsoft.com/math50">2</real>
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

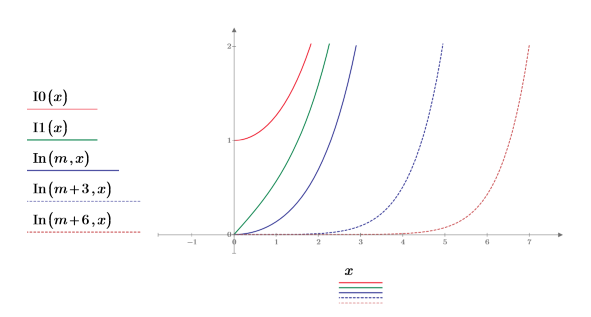
• Je höher die Ordnung der Funktion In, desto schärfer wird der Übergang von null bis unendlich.

• Nur die Funktion I0 hat ihren Ursprung bei (x=0,y=1). Alle Funktionen anderer Ordnung haben ihren Ursprung bei (x=0,y=0)..

4. Erstellen Sie ein Diagramm, um zu zeigen, dass I0(y)=In(0,y) Setzen Sie die Teilstrichwerte zurück, um die x-Achse zu vergrößern, damit mehr Details angezeigt werden:

<region id="ID0ENF66" actualWidth="572.46857242139" actualHeight="297.6" top="883.20000000000016" left="0" height="297.6" width="572.46857242139" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="68">
          <traceStyle color="#FFED1D2F" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
        <trace resultRef="69">
          <traceStyle color="#FF068149" symbol="circle" line-weight="1" line-style="None">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="438.06857242139" height="240" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="0" end="5">
          <axisLine position="origin" positionticmark="0" legendWidth="60.74" />
          <axisGrid>
            <gridFrequency>6</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <plotEquations>
            <plotEquation>
              <math>
                <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true" xmlns="http://schemas.mathsoft.com/math50">y</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <secondTickValue resultRef="70">
              <real xmlns="http://schemas.mathsoft.com/math50">1</real>
            </secondTickValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="0" end="2">
          <axisLine position="origin" positionticmark="0" legendWidth="105.416666666667" />
          <axisGrid>
            <gridFrequency>3</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <plotEquations>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">I0</id>
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">y</id>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">In</id>
                  <sequence>
                    <real>0</real>
                    <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">y</id>
                  </sequence>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="71">
              <real xmlns="http://schemas.mathsoft.com/math50">0</real>
            </startValue>
            <secondTickValue resultRef="72">
              <real xmlns="http://schemas.mathsoft.com/math50">1</real>
            </secondTickValue>
            <endValue resultRef="73">
              <real xmlns="http://schemas.mathsoft.com/math50">2</real>
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

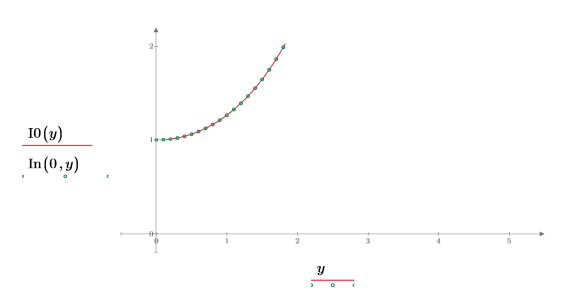
5. Erstellen Sie ein Diagramm, um zu zeigen, dass I1(y)=In(1,y) Setzen Sie die Teilstrichwerte zurück, um die x-Achse zu vergrößern, damit mehr Details angezeigt werden:

<region id="ID0EBH66" actualWidth="572.46857242139" actualHeight="297.6" top="1190.4" left="0" height="297.6" width="572.46857242139" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="74">
          <traceStyle color="#FFED1D2F" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
        <trace resultRef="75">
          <traceStyle color="#FF2E3192" symbol="circle" line-weight="1" line-style="None">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="438.06857242139" height="240" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="0" end="5">
          <axisLine position="origin" positionticmark="0" legendWidth="60.74" />
          <axisGrid>
            <gridFrequency>6</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <plotEquations>
            <plotEquation>
              <math>
                <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true" xmlns="http://schemas.mathsoft.com/math50">y</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <secondTickValue resultRef="76">
              <real xmlns="http://schemas.mathsoft.com/math50">1</real>
            </secondTickValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="0" end="2">
          <axisLine position="origin" positionticmark="0" legendWidth="105.416666666667" />
          <axisGrid>
            <gridFrequency>3</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <plotEquations>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">I1</id>
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">y</id>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">In</id>
                  <sequence>
                    <real>1</real>
                    <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">y</id>
                  </sequence>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="77">
              <real xmlns="http://schemas.mathsoft.com/math50">0</real>
            </startValue>
            <secondTickValue resultRef="78">
              <real xmlns="http://schemas.mathsoft.com/math50">1</real>
            </secondTickValue>
            <endValue resultRef="79">
              <real xmlns="http://schemas.mathsoft.com/math50">2</real>
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

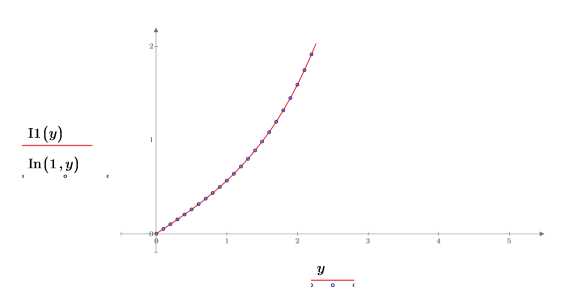
6. Verwenden Sie die symbolische Auswertung, um die Beziehung zwischen den einzelnen Funktionen und ihrer skalierten Version zu zeigen:

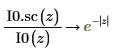
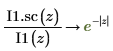
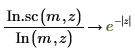
7. Verwenden Sie ein Diagramm, um Folgendes zu zeigen:

<region id="ID0ELL66" actualWidth="533.86857242139024" actualHeight="297.6" top="1785.6000000000004" left="0" height="297.6" width="533.86857242139024" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="84">
          <traceStyle color="#FFED1D2F" symbol="none" line-weight="1" line-style="Solid">Linien</traceStyle>
        </trace>
        <trace resultRef="85">
          <traceStyle color="#FF662D91" symbol="circle" line-weight="1" line-style="None">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="380.26857242139" height="240" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="0" end="5">
          <axisLine position="origin" positionticmark="0" legendWidth="60.74" />
          <axisGrid>
            <gridFrequency>6</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <plotEquations>
            <plotEquation>
              <math>
                <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true" xmlns="http://schemas.mathsoft.com/math50">y</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <secondTickValue resultRef="86">
              <real xmlns="http://schemas.mathsoft.com/math50">1</real>
            </secondTickValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="0" end="2">
          <axisLine position="origin" positionticmark="0" legendWidth="123.773333333333" />
          <axisGrid>
            <gridFrequency>3</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <plotEquations>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <mult />
                  <apply>
                    <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">I0</id>
                    <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">y</id>
                  </apply>
                  <apply>
                    <pow />
                    <id labels="CONSTANT" xml:space="preserve" label-is-contextual="true">e</id>
                    <apply>
                      <neg />
                      <apply>
                        <absval />
                        <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">y</id>
                      </apply>
                    </apply>
                  </apply>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <id labels="FUNCTION" xml:space="preserve">I0.sc</id>
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">y</id>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="87">
              <real xmlns="http://schemas.mathsoft.com/math50">0</real>
            </startValue>
            <secondTickValue resultRef="88">
              <real xmlns="http://schemas.mathsoft.com/math50">1</real>
            </secondTickValue>
            <endValue resultRef="89">
              <real xmlns="http://schemas.mathsoft.com/math50">2</real>
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

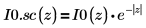
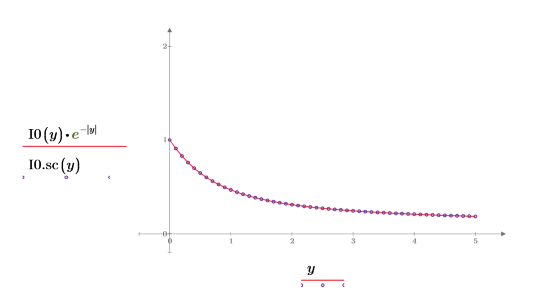
Die modifizierten Bessel-Funktionen der ersten Art haben keine Spitzenwerte.

Zugehörige Themen

Modifizierte (hyperbolische) Bessel-Funktionen

War dies hilfreich?