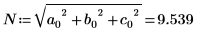Beispiel: Funktionen für Matrixnormen und -determinanten

Funktionen > Vektor und Matrix > Array-Eigenschaften > Beispiel: Funktionen für Matrixnormen und -determinanten

Beispiel: Funktionen für Matrixnormen und -determinanten

1. Definieren Sie eine quadratische Matrix.

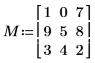
2. Legen Sie die Matrixelemente auf generische Variablennamen fest.

Zum Kopieren dieses Ausdrucks klicken

<region id="ID0E65DFB" actualWidth="111.93333333333334" actualHeight="69.37360000000001" top="230.40000000000003" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="44">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <matrix rows="3" cols="3">
        <id labels="VARIABLE" xml:space="preserve">
          <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">a<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
        </id>
        <id labels="VARIABLE" xml:space="preserve">
          <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">b<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
        </id>
        <id labels="VARIABLE" xml:space="preserve">
          <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">c<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
        </id>
        <id labels="VARIABLE" xml:space="preserve">
          <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">a<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript></Span>
        </id>
        <id labels="VARIABLE" xml:space="preserve">
          <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">b<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript></Span>
        </id>
        <id labels="VARIABLE" xml:space="preserve">
          <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">c<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript></Span>
        </id>
        <id labels="VARIABLE" xml:space="preserve">
          <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">a<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript></Span>
        </id>
        <id labels="VARIABLE" xml:space="preserve">
          <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">b<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript></Span>
        </id>
        <id labels="VARIABLE" xml:space="preserve">
          <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">c<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript></Span>
        </id>
      </matrix>
      <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">M</id>
    </define>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

3. Verwenden Sie die Funktion norm1, um die Norm L1 der Matrix M zu ermitteln.

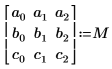
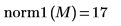
Alternativ können Sie die Norm L1 ermitteln, indem Sie das Maximum der absoluten Spaltensummen von M berechnen.

<region id="ID0EGCEFB" actualWidth="156.98000000000002" actualHeight="27.791200000000003" top="403.20000000000005" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="48">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id labels="VARIABLE" xml:space="preserve">
        <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">ACS<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
      </id>
      <apply>
        <plus />
        <apply>
          <plus />
          <apply>
            <absval />
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
              <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">a<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
            </id>
          </apply>
          <apply>
            <absval />
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
              <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">b<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
            </id>
          </apply>
        </apply>
        <apply>
          <absval />
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
            <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">c<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
          </id>
        </apply>
      </apply>
    </define>
  </math>
</region>

<region id="ID0EUCEFB" actualWidth="156.98000000000002" actualHeight="27.791200000000003" top="441.60000000000008" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="50">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id labels="VARIABLE" xml:space="preserve">
        <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">ACS<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript></Span>
      </id>
      <apply>
        <plus />
        <apply>
          <plus />
          <apply>
            <absval />
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
              <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">a<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript></Span>
            </id>
          </apply>
          <apply>
            <absval />
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
              <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">b<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript></Span>
            </id>
          </apply>
        </apply>
        <apply>
          <absval />
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
            <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">c<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript></Span>
          </id>
        </apply>
      </apply>
    </define>
  </math>
</region>

<region id="ID0ECDEFB" actualWidth="156.98000000000002" actualHeight="27.791200000000003" top="480.00000000000006" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="52">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id labels="VARIABLE" xml:space="preserve">
        <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">ACS<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript></Span>
      </id>
      <apply>
        <plus />
        <apply>
          <plus />
          <apply>
            <absval />
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
              <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">a<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript></Span>
            </id>
          </apply>
          <apply>
            <absval />
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
              <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">b<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript></Span>
            </id>
          </apply>
        </apply>
        <apply>
          <absval />
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
            <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">c<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript></Span>
          </id>
        </apply>
      </apply>
    </define>
  </math>
</region>

<region id="ID0EQDEFB" actualWidth="261.61666666666667" actualHeight="27.791200000000003" top="518.40000000000009" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="54">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id labels="VARIABLE" xml:space="preserve">
        <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">N<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">L1</Subscript></Span>
      </id>
      <eval>
        <apply>
          <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">max</id>
          <sequence>
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
              <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">ACS<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
            </id>
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
              <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">ACS<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript></Span>
            </id>
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
              <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">ACS<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript></Span>
            </id>
          </sequence>
        </apply>
        <unitOverride>
          <placeholder />
        </unitOverride>
      </eval>
    </define>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

4. Verwenden Sie die Funktion norm2, um die Norm L2 der Matrix M zu ermitteln.

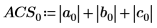
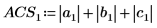
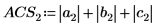
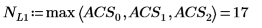
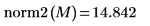
Verwenden Sie alternativ die Funktion svds, um den größten absoluten singulären Wert der Matrix M zu ermitteln.

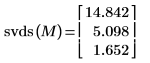
Die Funktion svds gibt einen Vektor von sortierten singulären Werten zurück, sodass der oberste Wert der größte singuläre Wert der Matrix M ist.

5. Verwenden Sie die Funktion norme, um die Euklid-Norm der Matrix M zu ermitteln.

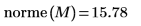
Berechnen Sie alternativ manuell die Quadratwurzel der Summe der absoluten Quadrate der Matrix M.

<region id="ID0E3JEFB" actualWidth="509.50600031296426" actualHeight="36.780453040075308" top="940.80000000000018" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="62">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id labels="VARIABLE" xml:space="preserve">
        <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">N<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">e</Subscript></Span>
      </id>
      <eval>
        <apply>
          <nthRoot />
          <placeholder />
          <apply>
            <plus />
            <apply>
              <plus />
              <apply>
                <plus />
                <apply>
                  <plus />
                  <apply>
                    <plus />
                    <apply>
                      <plus />
                      <apply>
                        <plus />
                        <apply>
                          <plus />
                          <apply>
                            <pow />
                            <apply>
                              <absval />
                              <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
                                <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">a<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
                              </id>
                            </apply>
                            <real>2</real>
                          </apply>
                          <apply>
                            <pow />
                            <apply>
                              <absval />
                              <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
                                <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">a<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript></Span>
                              </id>
                            </apply>
                            <real>2</real>
                          </apply>
                        </apply>
                        <apply>
                          <pow />
                          <apply>
                            <absval />
                            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
                              <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">a<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript></Span>
                            </id>
                          </apply>
                          <real>2</real>
                        </apply>
                      </apply>
                      <apply>
                        <pow />
                        <apply>
                          <absval />
                          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
                            <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">b<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
                          </id>
                        </apply>
                        <real>2</real>
                      </apply>
                    </apply>
                    <apply>
                      <pow />
                      <apply>
                        <absval />
                        <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
                          <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">b<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript></Span>
                        </id>
                      </apply>
                      <real>2</real>
                    </apply>
                  </apply>
                  <apply>
                    <pow />
                    <apply>
                      <absval />
                      <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
                        <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">b<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript></Span>
                      </id>
                    </apply>
                    <real>2</real>
                  </apply>
                </apply>
                <apply>
                  <pow />
                  <apply>
                    <absval />
                    <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
                      <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">c<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
                    </id>
                  </apply>
                  <real>2</real>
                </apply>
              </apply>
              <apply>
                <pow />
                <apply>
                  <absval />
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
                    <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">c<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript></Span>
                  </id>
                </apply>
                <real>2</real>
              </apply>
            </apply>
            <apply>
              <pow />
              <apply>
                <absval />
                <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
                  <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">c<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript></Span>
                </id>
              </apply>
              <real>2</real>
            </apply>
          </apply>
        </apply>
        <unitOverride>
          <placeholder />
        </unitOverride>
      </eval>
    </define>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

6. Verwenden Sie die Funktion normi, um die Unendlichnorm der Matrix M zu ermitteln.

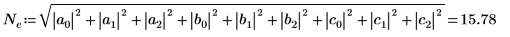
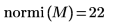
Verwenden Sie alternativ die max-Funktion, um das Maximum der absoluten Zeilensummen der Matrix M manuell zu berechnen.

<region id="ID0EUMEFB" actualWidth="158.77333333333334" actualHeight="27.791200000000003" top="1132.8000000000002" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="66">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id labels="VARIABLE" xml:space="preserve">
        <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">ARS<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
      </id>
      <apply>
        <plus />
        <apply>
          <plus />
          <apply>
            <absval />
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
              <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">a<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
            </id>
          </apply>
          <apply>
            <absval />
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
              <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">a<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript></Span>
            </id>
          </apply>
        </apply>
        <apply>
          <absval />
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
            <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">a<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript></Span>
          </id>
        </apply>
      </apply>
    </define>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

<region id="ID0ECNEFB" actualWidth="156.48333333333335" actualHeight="27.791200000000003" top="1171.2000000000003" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="68">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id labels="VARIABLE" xml:space="preserve">
        <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">ARS<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript></Span>
      </id>
      <apply>
        <plus />
        <apply>
          <plus />
          <apply>
            <absval />
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
              <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">b<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
            </id>
          </apply>
          <apply>
            <absval />
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
              <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">b<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript></Span>
            </id>
          </apply>
        </apply>
        <apply>
          <absval />
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
            <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">b<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript></Span>
          </id>
        </apply>
      </apply>
    </define>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

<region id="ID0EQNEFB" actualWidth="155.11333333333334" actualHeight="27.791200000000003" top="1209.6000000000001" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="70">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id labels="VARIABLE" xml:space="preserve">
        <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">ARS<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript></Span>
      </id>
      <apply>
        <plus />
        <apply>
          <plus />
          <apply>
            <absval />
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
              <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">c<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
            </id>
          </apply>
          <apply>
            <absval />
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
              <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">c<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript></Span>
            </id>
          </apply>
        </apply>
        <apply>
          <absval />
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
            <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">c<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript></Span>
          </id>
        </apply>
      </apply>
    </define>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

<region id="ID0E5NEFB" actualWidth="252.23666666666671" actualHeight="27.791200000000003" top="1248.0000000000002" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="72">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id labels="VARIABLE" xml:space="preserve">
        <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">N<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">i</Subscript></Span>
      </id>
      <eval>
        <apply>
          <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">max</id>
          <sequence>
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
              <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">ARS<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
            </id>
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
              <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">ARS<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript></Span>
            </id>
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
              <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">ARS<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript></Span>
            </id>
          </sequence>
        </apply>
        <unitOverride>
          <placeholder />
        </unitOverride>
      </eval>
    </define>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

7. Verwenden Sie die Funktion det, um die Determinante der Matrix M zu ermitteln.

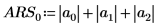
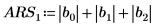
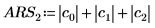
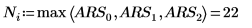
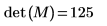
Berechnen Sie alternativ die Determinante der Matrix M manuell.

<region id="ID0EWQEFB" actualWidth="490.83" actualHeight="27.791200000000003" top="1401.6000000000001" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="76">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id labels="VARIABLE" xml:space="preserve">DET</id>
      <eval>
        <apply>
          <plus />
          <apply>
            <minus />
            <apply>
              <mult />
              <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
                <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">a<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
              </id>
              <parens>
                <apply>
                  <minus />
                  <apply>
                    <mult />
                    <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
                      <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">b<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript></Span>
                    </id>
                    <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
                      <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">c<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript></Span>
                    </id>
                  </apply>
                  <apply>
                    <mult />
                    <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
                      <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">b<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript></Span>
                    </id>
                    <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
                      <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">c<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript></Span>
                    </id>
                  </apply>
                </apply>
              </parens>
            </apply>
            <apply>
              <mult />
              <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
                <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">a<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript></Span>
              </id>
              <parens>
                <apply>
                  <minus />
                  <apply>
                    <mult />
                    <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
                      <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">b<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
                    </id>
                    <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
                      <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">c<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript></Span>
                    </id>
                  </apply>
                  <apply>
                    <mult />
                    <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
                      <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">b<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript></Span>
                    </id>
                    <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
                      <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">c<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
                    </id>
                  </apply>
                </apply>
              </parens>
            </apply>
          </apply>
          <apply>
            <mult />
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
              <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">a<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript></Span>
            </id>
            <parens>
              <apply>
                <minus />
                <apply>
                  <mult />
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
                    <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">b<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
                  </id>
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
                    <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">c<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript></Span>
                  </id>
                </apply>
                <apply>
                  <mult />
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
                    <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">b<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript></Span>
                  </id>
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
                    <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">c<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
                  </id>
                </apply>
              </apply>
            </parens>
          </apply>
        </apply>
        <unitOverride>
          <placeholder />
        </unitOverride>
      </eval>
    </define>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

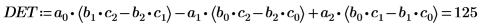
8. Verwenden Sie die Funktion norm, um die Norm eines Vektors zu ermitteln, der die Elemente der Spalte 0 der Matrix M enthält.

Zum Kopieren dieses Ausdrucks klicken

<region id="ID0E3SEFB" actualWidth="109.26666666666668" actualHeight="69.37360000000001" top="1497.6000000000001" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="78">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id labels="VARIABLE" xml:space="preserve">v</id>
      <eval>
        <matrix rows="3" cols="1">
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
            <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">a<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
          </id>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
            <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">b<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
          </id>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
            <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">c<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
          </id>
        </matrix>
        <unitOverride>
          <placeholder />
        </unitOverride>
      </eval>
    </define>
  </math>
</region>

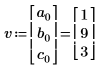
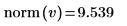
Berechnen Sie alternativ die Norm des Vektors v manuell.

<region id="ID0EBUEFB" actualWidth="207.04933364629747" actualHeight="36.780453040075308" top="1632.0000000000002" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="82">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id labels="VARIABLE" xml:space="preserve">N</id>
      <eval>
        <apply>
          <nthRoot />
          <placeholder />
          <apply>
            <plus />
            <apply>
              <plus />
              <apply>
                <pow />
                <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
                  <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">a<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
                </id>
                <real>2</real>
              </apply>
              <apply>
                <pow />
                <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
                  <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">b<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
                </id>
                <real>2</real>
              </apply>
            </apply>
            <apply>
              <pow />
              <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
                <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">c<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
              </id>
              <real>2</real>
            </apply>
          </apply>
        </apply>
        <unitOverride>
          <placeholder />
        </unitOverride>
      </eval>
    </define>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

Zugehörige Themen

Norm einer quadratischen Matrix

War dies hilfreich?