Beispiel: Lokale Kosinus-Transformation

Funktionen > Transformationen und Filter > Beispiel: Lokale Kosinus-Transformation

1. Definieren Sie ein Testsignal durch Verketten von vier Sinuskurven, die vier unterschiedliche Frequenzen aufweisen.

<region id="ID0EWTXDB" top="96.000000000000014" left="38.400000000000006" height="25.6" width="58.13000000000001" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="145"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve">n</id> <real>512</real> </define> </math> </region>
<region id="ID0EXUXDB" top="134.40000000000003" left="38.400000000000006" height="27.791200000000003" width="53.580000000000005" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="147"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve"> <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">f<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span> </id> <real>32</real> </define> </math> </region>	<region id="ID0EMVXDB" top="134.40000000000003" left="134.40000000000003" height="49.391200000000005" width="58.433333333333337" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="149"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve"> <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">ω<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span> </id> <apply> <div /> <real>1</real> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true"> <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">f<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span> </id> </apply> </define> </math> </region>
<region id="ID0EGWXDB" top="172.8" left="38.400000000000006" height="47.2" width="89.13" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="151"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve">i</id> <range> <real>0</real> <apply> <minus /> <apply> <div /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">n</id> <real>4</real> </apply> <real>1</real> </apply> </range> </define> </math> </region>	<region id="ID0E2WXDB" top="172.8" left="192.00000000000003" height="36.800000000000004" width="155.33" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="153"> <define xmlns="http://schemas.mathsoft.com/math50"> <apply> <indexer /> <id labels="VARIABLE" xml:space="preserve">y</id> <id labels="*" xml:space="preserve">i</id> </apply> <apply> <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">cos</id> <apply> <mult /> <apply> <mult /> <apply> <mult /> <apply> <mult /> <real>2</real> <id labels="CONSTANT" xml:space="preserve" label-is-contextual="true">π</id> </apply> <id xml:space="preserve">i</id> </apply> <real>1</real> </apply> <id labels="VARIABLE" xml:space="preserve"> <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">ω<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span> </id> </apply> </apply> </define> </math> </region>
<region id="ID0EVXXDB" top="230.40000000000003" left="38.400000000000006" height="47.2" width="96.36333333333333" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="155"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve">j</id> <range> <apply> <div /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">n</id> <real>4</real> </apply> <apply> <minus /> <apply> <div /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">n</id> <real>2</real> </apply> <real>1</real> </apply> </range> </define> </math> </region>	<region id="ID0EKYXDB" top="230.40000000000003" left="192.00000000000003" height="36.800000000000004" width="157.2" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="157"> <define xmlns="http://schemas.mathsoft.com/math50"> <apply> <indexer /> <id labels="VARIABLE" xml:space="preserve">y</id> <id labels="*" xml:space="preserve">j</id> </apply> <apply> <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">cos</id> <apply> <mult /> <apply> <mult /> <apply> <mult /> <apply> <mult /> <real>2</real> <id labels="CONSTANT" xml:space="preserve" label-is-contextual="true">π</id> </apply> <id xml:space="preserve">j</id> </apply> <real>5</real> </apply> <id labels="VARIABLE" xml:space="preserve"> <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">ω<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span> </id> </apply> </apply> </define> </math> </region>
<region id="ID0EEZXDB" top="288.00000000000006" left="38.400000000000006" height="47.2" width="115.34" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="159"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve">k</id> <range> <apply> <div /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">n</id> <real>2</real> </apply> <apply> <minus /> <apply> <div /> <apply> <mult /> <real>3</real> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">n</id> </apply> <real>4</real> </apply> <real>1</real> </apply> </range> </define> </math> </region>	<region id="ID0EZZXDB" top="288.00000000000006" left="192.00000000000003" height="36.800000000000004" width="168.64" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="161"> <define xmlns="http://schemas.mathsoft.com/math50"> <apply> <indexer /> <id labels="VARIABLE" xml:space="preserve">y</id> <id labels="*" xml:space="preserve">k</id> </apply> <apply> <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">cos</id> <apply> <mult /> <apply> <mult /> <apply> <mult /> <apply> <mult /> <real>2</real> <id labels="CONSTANT" xml:space="preserve" label-is-contextual="true">π</id> </apply> <id xml:space="preserve">k</id> </apply> <real>10</real> </apply> <id labels="VARIABLE" xml:space="preserve"> <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">ω<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span> </id> </apply> </apply> </define> </math> </region>
<region id="ID0ES1XDB" top="345.6" left="38.400000000000006" height="47.2" width="106.81333333333335" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="163"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve">l</id> <range> <apply> <mult /> <real>3</real> <apply> <div /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">n</id> <real>4</real> </apply> </apply> <apply> <minus /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">n</id> <real>1</real> </apply> </range> </define> </math> </region>	<region id="ID0EG2XDB" top="345.6" left="192.00000000000003" height="36.800000000000004" width="162.54" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="165"> <define xmlns="http://schemas.mathsoft.com/math50"> <apply> <indexer /> <id labels="VARIABLE" xml:space="preserve">y</id> <id labels="*" xml:space="preserve">l</id> </apply> <apply> <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">cos</id> <apply> <mult /> <apply> <mult /> <apply> <mult /> <apply> <mult /> <real>2</real> <id labels="CONSTANT" xml:space="preserve" label-is-contextual="true">π</id> </apply> <id xml:space="preserve">l</id> </apply> <real>15</real> </apply> <id labels="VARIABLE" xml:space="preserve"> <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">ω<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span> </id> </apply> </apply> </define> </math> </region>

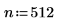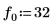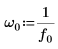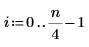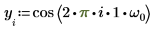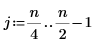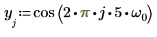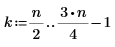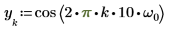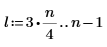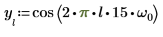2. Plotten Sie das Testsignal.

<region id="ID0EI4XDB" top="441.60000000000008" left="38.400000000000006" height="278.40000658035285" width="576.80001323223109" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="169">
          <traceStyle color="#FFFF0000" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="476.800013232231" height="220.800006580353" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="0" end="550">
          <axisLine position="origin" positionticmark="5" legendWidth="61.0033333333333" />
          <axisGrid>
            <gridFrequency>12</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="172">
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">p</id>
              </math>
              <math resultRef="173">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue resultRef="171">
              <apply xmlns="http://schemas.mathsoft.com/math50">
                <minus />
                <id xml:space="preserve">n</id>
                <real>1</real>
              </apply>
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="-1" end="1">
          <axisLine position="origin" positionticmark="0" legendWidth="66.1633333333333" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="174">
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <indexer />
                  <id xml:space="preserve">y</id>
                  <id xml:space="preserve">p</id>
                </apply>
              </math>
              <math resultRef="175">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

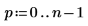
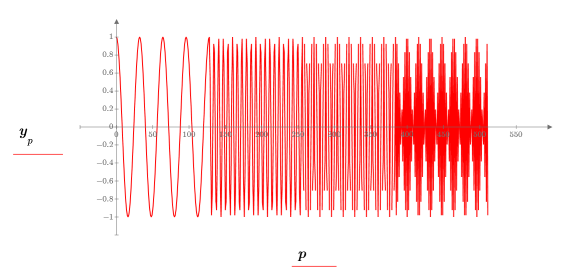
3. Verwenden Sie die Funktion cpt, um die lokale Vorwärts-Kosinustransformation der Ebene 2 zu berechnen.

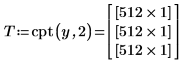
Die zurückgegebene Matrix enthält die drei Ebenen der lokalen Kosinustransformation.

Block auf Ebene 0:	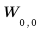<region id="ID0E4BYDB" top="921.60000000000014" left="307.20000000000005" height="36.800000000000004" width="40.436666666666667" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="183"> <apply xmlns="http://schemas.mathsoft.com/math50"> <indexer /> <id xml:space="preserve">W</id> <sequence> <real>0</real> <real>0</real> </sequence> </apply> </math> </region>
Block auf Ebene 1:	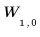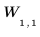<region id="ID0ECDYDB" top="960.00000000000011" left="230.40000000000003" height="36.800000000000004" width="40.436666666666667" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="185"> <apply xmlns="http://schemas.mathsoft.com/math50"> <indexer /> <id xml:space="preserve">W</id> <sequence> <real>1</real> <real>0</real> </sequence> </apply> </math> </region>		<region id="ID0EYDYDB" top="960.00000000000011" left="384.00000000000006" height="36.800000000000004" width="40.436666666666667" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="187"> <apply xmlns="http://schemas.mathsoft.com/math50"> <indexer /> <id xml:space="preserve">W</id> <sequence> <real>1</real> <real>1</real> </sequence> </apply> </math> </region>
Block auf Ebene 2:	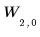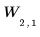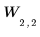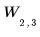<region id="ID0E2EYDB" top="998.40000000000009" left="192.00000000000003" height="36.800000000000004" width="40.436666666666667" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="189"> <apply xmlns="http://schemas.mathsoft.com/math50"> <indexer /> <id xml:space="preserve">W</id> <sequence> <real>2</real> <real>0</real> </sequence> </apply> </math> </region>	<region id="ID0EPFYDB" top="998.40000000000009" left="268.80000000000007" height="36.800000000000004" width="40.436666666666667" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="191"> <apply xmlns="http://schemas.mathsoft.com/math50"> <indexer /> <id xml:space="preserve">W</id> <sequence> <real>2</real> <real>1</real> </sequence> </apply> </math> </region>	<region id="ID0EDGYDB" top="998.40000000000009" left="345.6" height="36.800000000000004" width="40.436666666666667" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="193"> <apply xmlns="http://schemas.mathsoft.com/math50"> <indexer /> <id xml:space="preserve">W</id> <sequence> <real>2</real> <real>2</real> </sequence> </apply> </math> </region>	<region id="ID0EXGYDB" top="998.40000000000009" left="422.40000000000009" height="36.800000000000004" width="40.436666666666667" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="195"> <apply xmlns="http://schemas.mathsoft.com/math50"> <indexer /> <id xml:space="preserve">W</id> <sequence> <real>2</real> <real>3</real> </sequence> </apply> </math> </region>

4. Plotten Sie Ebene 0 der Transformation, die die diskrete Kosinustransformation (DCT) des einzelnen verjüngten Datenblocks enthält.

<region id="ID0ELIYDB" top="1094.4" left="38.400000000000006" height="230.40000514984129" width="576.00001323223114" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="197">
          <traceStyle color="#FFFF0000" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="456.800013232231" height="172.800005149841" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="0" end="550">
          <axisLine position="origin" positionticmark="4" legendWidth="61.0033333333333" />
          <axisGrid>
            <gridFrequency>12</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers>
            <marker resultRef="198" display="true" color="#FF068149" line-style="Dot" value="32">
              <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">
                <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">f<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
              </id>
            </marker>
            <marker resultRef="200" display="true" color="#FF068149" line-style="Dot" value="160">
              <apply xmlns="http://schemas.mathsoft.com/math50">
                <mult />
                <real>5</real>
                <id xml:space="preserve">
                  <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">f<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
                </id>
              </apply>
            </marker>
            <marker resultRef="202" display="true" color="#FF068149" line-style="Dot" value="480">
              <apply xmlns="http://schemas.mathsoft.com/math50">
                <mult />
                <real>15</real>
                <id xml:space="preserve">
                  <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">f<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
                </id>
              </apply>
            </marker>
            <marker resultRef="204" display="true" color="#FF068149" line-style="Dot" value="320">
              <apply xmlns="http://schemas.mathsoft.com/math50">
                <mult />
                <real>10</real>
                <id xml:space="preserve">
                  <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">f<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
                </id>
              </apply>
            </marker>
          </markers>
          <numberFormat>
            <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="208">
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">p</id>
              </math>
              <math resultRef="209">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue resultRef="207">
              <apply xmlns="http://schemas.mathsoft.com/math50">
                <minus />
                <id xml:space="preserve">n</id>
                <real>1</real>
              </apply>
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="-4" end="4">
          <axisLine position="origin" positionticmark="0" legendWidth="85.76" />
          <axisGrid>
            <gridFrequency>9</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="214">
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <indexer />
                  <parens>
                    <apply>
                      <indexer />
                      <id xml:space="preserve">T</id>
                      <real>0</real>
                    </apply>
                  </parens>
                  <id xml:space="preserve">p</id>
                </apply>
              </math>
              <math resultRef="215">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="211">
              <real xmlns="http://schemas.mathsoft.com/math50">-4</real>
            </startValue>
            <secondTickValue resultRef="213">
              <real xmlns="http://schemas.mathsoft.com/math50">-3</real>
            </secondTickValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

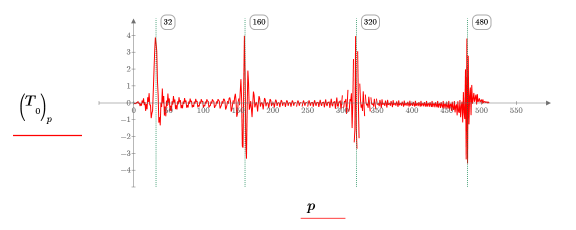
Die Transformation enthält vier Spitzenwerte, die den Frequenzen der vier Sinuskurven entsprechen.

5. Plotten Sie Ebene 1 der Transformation, die zwei diskrete Kosinustransformationen enthält, eine für die erste Hälfte der Daten und eine für die zweite Hälfte.

<region id="ID0E6JYDB" top="1459.2000000000003" left="38.400000000000006" height="240.00000543594365" width="576.40001294612875" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="227">
          <traceStyle color="#FFFF0000" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="457.200012946129" height="182.400005435944" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="0" end="550">
          <axisLine position="origin" positionticmark="5" legendWidth="61.0033333333333" />
          <axisGrid>
            <gridFrequency>12</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers>
            <marker resultRef="228" display="true" color="#FF068149" line-style="Dot" value="16">
              <apply xmlns="http://schemas.mathsoft.com/math50">
                <div />
                <id xml:space="preserve">
                  <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">f<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
                </id>
                <real>2</real>
              </apply>
            </marker>
            <marker resultRef="230" display="true" color="#FF068149" line-style="Dot" value="80">
              <apply xmlns="http://schemas.mathsoft.com/math50">
                <div />
                <apply>
                  <mult />
                  <real>5</real>
                  <id xml:space="preserve">
                    <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">f<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
                  </id>
                </apply>
                <real>2</real>
              </apply>
            </marker>
            <marker resultRef="232" display="true" color="#FF068149" line-style="Dot" value="160">
              <apply xmlns="http://schemas.mathsoft.com/math50">
                <div />
                <apply>
                  <mult />
                  <real>10</real>
                  <id xml:space="preserve">
                    <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">f<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
                  </id>
                </apply>
                <real>2</real>
              </apply>
            </marker>
            <marker resultRef="234" display="true" color="#FF068149" line-style="Dot" value="496">
              <apply xmlns="http://schemas.mathsoft.com/math50">
                <plus />
                <apply>
                  <div />
                  <id xml:space="preserve">n</id>
                  <real>2</real>
                </apply>
                <apply>
                  <div />
                  <apply>
                    <scale />
                    <real>15</real>
                    <id xml:space="preserve">
                      <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">f<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
                    </id>
                  </apply>
                  <real>2</real>
                </apply>
              </apply>
            </marker>
            <marker resultRef="236" display="true" color="#FF2E3192" line-style="Dash" value="256">
              <apply xmlns="http://schemas.mathsoft.com/math50">
                <div />
                <id xml:space="preserve">n</id>
                <real>2</real>
              </apply>
            </marker>
            <marker resultRef="238" display="true" color="#FF068149" line-style="Dot" value="416">
              <apply xmlns="http://schemas.mathsoft.com/math50">
                <plus />
                <apply>
                  <div />
                  <id xml:space="preserve">n</id>
                  <real>2</real>
                </apply>
                <apply>
                  <div />
                  <apply>
                    <scale />
                    <real>10</real>
                    <id xml:space="preserve">
                      <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">f<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
                    </id>
                  </apply>
                  <real>2</real>
                </apply>
              </apply>
            </marker>
          </markers>
          <numberFormat>
            <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="242">
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">p</id>
              </math>
              <math resultRef="243">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue resultRef="241">
              <apply xmlns="http://schemas.mathsoft.com/math50">
                <minus />
                <id xml:space="preserve">n</id>
                <real>1</real>
              </apply>
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="-5" end="6">
          <axisLine position="origin" positionticmark="0" legendWidth="85.76" />
          <axisGrid>
            <gridFrequency>12</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="244">
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <indexer />
                  <parens>
                    <apply>
                      <indexer />
                      <id xml:space="preserve">T</id>
                      <real>1</real>
                    </apply>
                  </parens>
                  <id xml:space="preserve">p</id>
                </apply>
              </math>
              <math resultRef="245">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

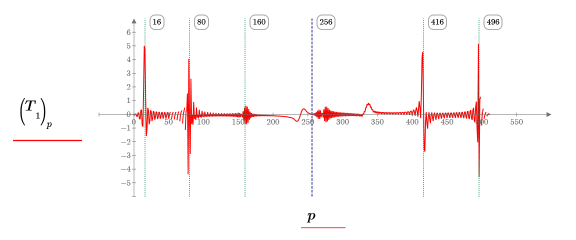
Die Transformation enthält zwei Spitzenwerte in jeder der beiden diskreten Kosinustransformationen mit n/2 Datenpunkten. Wenn Sie auf die vertikalen Markierungen klicken, wird angezeigt, dass die ersten beiden auf bei der halben Frequenz der ersten beiden Sinuskurven und die beiden zweiten bei (n/2) + der Hälfte der Frequenz der beiden zweiten Sinuskurven liegen. Die blaue Markierung zeigt die Grenze zwischen den beiden diskreten Kosinustransformationen an.

6. Plotten Sie Ebene 2 der Transformation, die die vier diskreten Kosinustransformationen enthält, jeweils eine für jedes der vier Datenviertel.

<region id="ID0E3LYDB" top="1920.0000000000002" left="38.400000000000006" height="240.000005435944" width="576.400012946129" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="257">
          <traceStyle color="#FFFF0000" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="457.200012946129" height="182.400005435944" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="0" end="550">
          <axisLine position="origin" positionticmark="5" legendWidth="61.0033333333333" />
          <axisGrid>
            <gridFrequency>12</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers>
            <marker resultRef="258" display="true" color="#FF068149" line-style="Dot" value="8">
              <apply xmlns="http://schemas.mathsoft.com/math50">
                <div />
                <id xml:space="preserve">
                  <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">f<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
                </id>
                <real>4</real>
              </apply>
            </marker>
            <marker resultRef="260" display="true" color="#FF068149" line-style="Dot" value="168">
              <apply xmlns="http://schemas.mathsoft.com/math50">
                <plus />
                <apply>
                  <div />
                  <id xml:space="preserve">n</id>
                  <real>4</real>
                </apply>
                <apply>
                  <mult />
                  <real>5</real>
                  <apply>
                    <div />
                    <id xml:space="preserve">
                      <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">f<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
                    </id>
                    <real>4</real>
                  </apply>
                </apply>
              </apply>
            </marker>
            <marker resultRef="262" display="true" color="#FF068149" line-style="Dot" value="336">
              <apply xmlns="http://schemas.mathsoft.com/math50">
                <plus />
                <apply>
                  <div />
                  <id xml:space="preserve">n</id>
                  <real>2</real>
                </apply>
                <apply>
                  <mult />
                  <real>10</real>
                  <apply>
                    <div />
                    <id xml:space="preserve">
                      <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">f<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
                    </id>
                    <real>4</real>
                  </apply>
                </apply>
              </apply>
            </marker>
            <marker resultRef="264" display="true" color="#FF068149" line-style="Dot" value="504">
              <apply xmlns="http://schemas.mathsoft.com/math50">
                <plus />
                <apply>
                  <div />
                  <apply>
                    <scale />
                    <real>3</real>
                    <id xml:space="preserve">n</id>
                  </apply>
                  <real>4</real>
                </apply>
                <apply>
                  <mult />
                  <real>15</real>
                  <apply>
                    <div />
                    <id xml:space="preserve">
                      <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">f<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
                    </id>
                    <real>4</real>
                  </apply>
                </apply>
              </apply>
            </marker>
            <marker resultRef="266" display="true" color="#FF2E3192" line-style="Dash" value="128">
              <apply xmlns="http://schemas.mathsoft.com/math50">
                <div />
                <id xml:space="preserve">n</id>
                <real>4</real>
              </apply>
            </marker>
            <marker resultRef="268" display="true" color="#FF2E3192" line-style="Dash" value="256">
              <apply xmlns="http://schemas.mathsoft.com/math50">
                <div />
                <id xml:space="preserve">n</id>
                <real>2</real>
              </apply>
            </marker>
            <marker resultRef="270" display="true" color="#FF2E3192" line-style="Dash" value="384">
              <apply xmlns="http://schemas.mathsoft.com/math50">
                <div />
                <apply>
                  <scale />
                  <real>3</real>
                  <id xml:space="preserve">n</id>
                </apply>
                <real>4</real>
              </apply>
            </marker>
          </markers>
          <numberFormat>
            <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="274">
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">p</id>
              </math>
              <math resultRef="275">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue resultRef="273">
              <apply xmlns="http://schemas.mathsoft.com/math50">
                <minus />
                <id xml:space="preserve">n</id>
                <real>1</real>
              </apply>
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="-5" end="7">
          <axisLine position="origin" positionticmark="0" legendWidth="85.76" />
          <axisGrid>
            <gridFrequency>13</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="276">
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <indexer />
                  <parens>
                    <apply>
                      <indexer />
                      <id xml:space="preserve">T</id>
                      <real>2</real>
                    </apply>
                  </parens>
                  <id xml:space="preserve">p</id>
                </apply>
              </math>
              <math resultRef="277">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

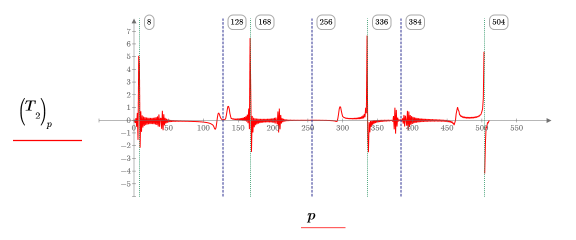
Die Transformation enthält einen Spitzenwert in jeder der vier diskreten Kosinustransformationen mit n/4 Datenpunkten. Wenn Sie auf die vertikalen Markierungen klicken, wird angezeigt, dass der erste Spitzenwert beim Viertel der Frequenz der ersten Sinuskurve liegt, der zweiten Spitzenwert bei n/4 + ein Viertel der Frequenz der zweiten Sinuskurve, der dritten Spitzenwert bei 2n/4 + ein Viertel der Frequenz der dritten Sinuskurve und der vierten Spitzenwert bei 3n/4 + ein Viertel der Frequenz der vierten Sinuskurve. Die blauen Markierungen zeigen die Grenzen zwischen den vier diskreten Kosinustransformationen.

Zugehörige Themen

Lokale Kosinustransformationen

War dies hilfreich?