Beispiel: Kleinste-Quadrate-Spline
Spline2, Binterp und DWS
Verwenden Sie die Funktion Spline2, um den optimalen Knotensatz zu ermitteln, den Binterp benötigt, um eine Spline-Interpolation der kleinsten Quadrate zu berechnen.
1. Definieren Sie einen Datensatz.

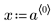 | 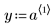 | 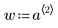 |
w ist ein Vektor von Gewichtungen, die die geschätzten Standardabweichungen des Zufallsfehlers in y angeben.
2. Definieren Sie den Grad der gewünschten Spline-Polynome.
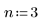
3. Rufen Sie die Funktion Spline2 auf.
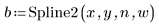

Das erste Element von Vektor b gibt die Ordnung des B-Splines an. Das zweite Element gibt die Anzahl an Intervallen von (knots - 1) an. Die nächsten Elemente geben die Knotenwerte an. Die verbleibenden Elemente enthalten die Koeffizienten für die B-Spline-Basisfunktionen.
Der erste und der letzte Knoten entsprechen den Endpunkten der ursprünglichen x-Daten, wenn die Knoten automatisch generiert wurden:
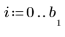
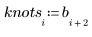
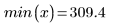 | 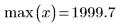 |
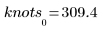 | 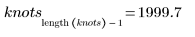 |
4. Rufen Sie die Funktion Binterp auf, um einen Wertebereich abzurufen, der dem Bereich von x entspricht.
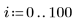
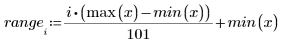

Zeile i von spline1 enthält den interpolierten Wert und die erste, zweite und dritte Ableitung an dem im Bereich i definierten Punkt.
5. Stellen Sie die ursprünglichen Daten und den interpolierten Spline grafisch dar.
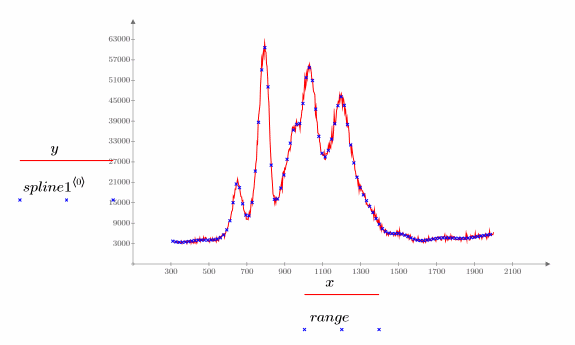
Die optimale Anzahl an Knoten und deren Abstand werden durch die Durbin-Watson-Statistik bestimmt. Diese Statistik sollte für eine gute Anpassung den Wert 2 aufweisen. Diese Statistik kann mithilfe der Funktion DWS oder durch Extrahieren des entsprechenden Elements aus Matrix b ermittelt werden:
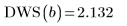
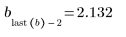
6. Verwenden Sie das optionale letzte Argument von Spline2, ein Prozentsatz von 0 bis 1, um ein Signifikanzniveau oder eine Ablehnungsgrenze für den Durbin-Watson-Test anzugeben.
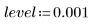
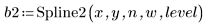
Im Allgemeinen führen höhere Ablehnungsgrenzen zu mehr Knoten und umfangreicheren Berechnungen. Dies ist jedoch nicht immer der Fall.
7. Berechnen Sie die Anzahl an Knoten, die von Spline2 verwendet werden.
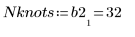
8. Rufen Sie die Funktion DWS auf, um die Durbin-Watson-Statistik zu berechnen.
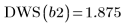
9. Stellen Sie die beiden interpolierten Splines grafisch dar.
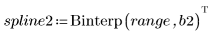
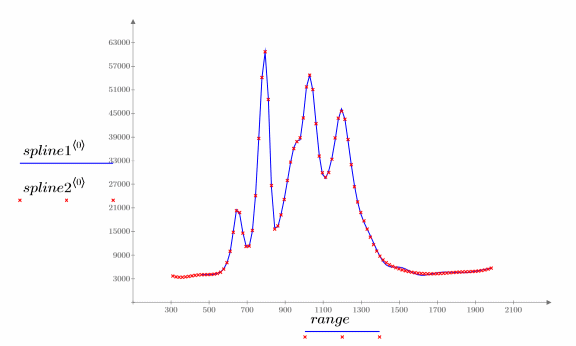
Sie können die Interpolation ohne Gewichtung durchführen:
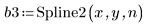
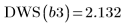
Sie können die Interpolation ohne Gewichtung, aber mit Ablehnungsgrenze durchführen:
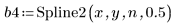
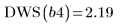
Spline-Ableitungen
Stellen Sie die ersten drei Ableitungen des Interpolations-Splines grafisch dar.
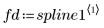
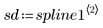
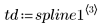
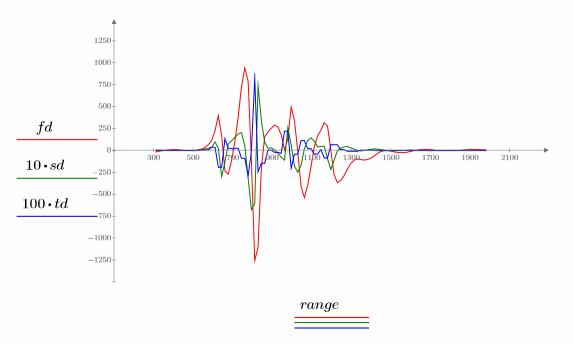
Angeben eigener Knoten
Sie können für die B-Spline-Interpolation Ihre eigenen Knoten angeben.
1. Definieren Sie eine Zeichenfolge mit Knoten.
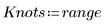
2. Stellen Sie den interpolierten Spline grafisch dar.
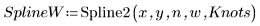
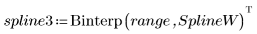
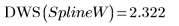
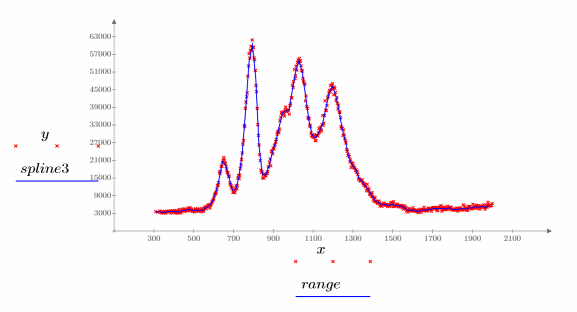
Sie können Knoten ohne Gewichtungsvektor angeben:

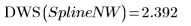
Ausreißer
Sie können die Auswirkungen des Entfernens eines Ausreißers aus der Spline-Interpolation anzeigen.
1. Rufen Sie die Funktion GrubbsClassic auf, um den Punkt zu ermitteln, bei dem es sich um den wahrscheinlichsten Ausreißer handelt.

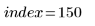
Ein verdächtiger Punkt befindet sich ganz oben an der zweiten Datenspitze.
2. Entfernen Sie den Punkt aus dem Datensatz und aus der Weighing-Funktion.
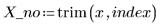
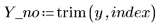
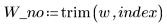
3. Rufen Sie die Funktion Spline2 für den neuen Datensatz auf.
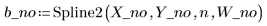
Gemäß der Durbin-Watson-Statistik hat sich die Anpassung verbessert.
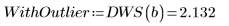
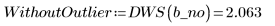
4. Vergleichen Sie die Ergebnisse der Interpolationen am verdächtigen Datenwert:
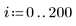
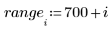
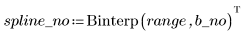
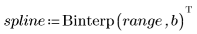
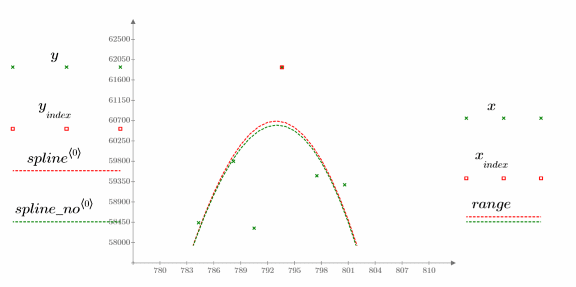
Der Spline fällt leicht ab, nachdem der Ausreißer entfernt wurde.