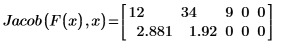Beispiel: Jacob-Funktion
Verwenden Sie die Funktion Jacob, um den Jacobian-Wert einer Vektorfunktion zu berechnen, geschrieben als Spaltenvektor von reellwertigen Funktionen.
1. Definieren Sie die beiden im Vektor F enthaltenen Funktionen:
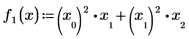
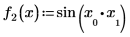
2. Definieren Sie den Vektor F:
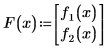
3. Da die Variablen numerisch nicht definiert sind, werten Sie Jacob symbolisch aus.
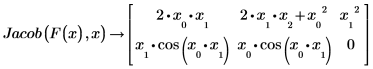
◦ Die Zeile 0 der Matrix enthält drei Elemente: die partielle Ableitung von f1 in Bezug auf x0, die partielle Ableitung in Bezug auf x1 und die partielle Ableitung in Bezug auf x2.
◦ Entsprechend enthält Zeile 1 drei Elemente: die partielle Ableitung von f2 in Bezug auf x0, die partielle Ableitung in Bezug auf x1 und die partielle Ableitung in Bezug auf x2.
PTC Mathcad nimmt an, dass die Anzahl der Variablen gleich maxsub + 1 ist; dabei ist maxsub der größte tiefgestellte Index, der unter den Variablen in den Funktionen angezeigt wird. |
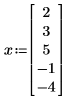
4. Weisen Sie den Variablen numerische Werte zu, und werten Sie die Funktion Jacob anschließend numerisch aus:
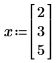
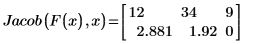
Zusätzliche Variablen angeben, die in den Funktionen nicht angezeigt werden
1. Erzwingen Sie, dass die Anzahl der Spalten in der resultierenden Matrix größer ist als die Anzahl der Variablen, indem Sie das optionale dritte Argument von Jacob festlegen:
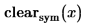
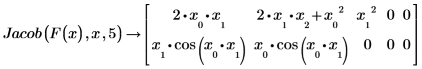
2. Erzwingen Sie, dass die Anzahl der Spalten in der resultierenden Matrix größer ist als die Anzahl der Variablen, indem Sie Werte für nicht vorhandene Variablen angeben: