Beispiel: Wärmefluss auf einer quadratischen Platte

Funktionen > Lösen und Optimieren > Lösungsalgorithmen für Differentialgleichungen > Beispiel: Wärmefluss auf einer quadratischen Platte - II

Beispiel: Wärmefluss auf einer quadratischen Platte - II

Lösen Sie die Gleichung für die Beharrungstemperaturverteilung einer quadratischen Platte mit dem Gleichungslöser für partielle Differentialgleichungen relax.

Poisson-Gleichung lösen

Lösen Sie die Wärmegleichung auf, bei der die Werte der Quellfunktion bekannt und die Randbedingungen ungleich null sind.

Die Funktion relax beruht auf einer völlig anderen Lösungsmethode und verlangt daher einen anderen Satz von Argumenten.

1. Definieren Sie fünf quadratische Matrizen a, b, c, d und e, die die Koeffizienten für die Laplace-Näherung zu enthalten:

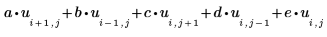
Diese Arrays können eine beliebige von Ihnen festgelegte Größe haben. Je größer sie sind, desto feiner ist das Netz in der Lösung.

2. Definieren Sie die Bemaßung der quadratischen Platte:

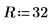
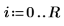
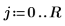
3. Legen Sie die Koeffizienten fest:

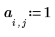
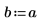
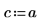
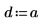
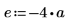
4. Legen Sie die Kraft und Position einer konstanten Quelle fest.

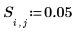
5. Legen Sie eine quadratische Matrix f fest, deren Größe derjenigen des Rasters entspricht und die die bekannten Grenzwerte der Funktion F(x,y) sowie die Schätzwerte für die unbekannten Innenwerte enthält.

◦ Randbedingung entlang der Oberseite:

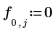
◦ Randbedingung entlang der Unterseite:

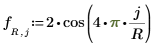
◦ Randbedingung entlang der Kanten:

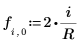
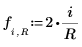
6. Definieren Sie die Variable r, eine reelle Zahl zwischen 0 und 1, für Jacobi spectral radius.

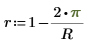
Dieser Parameter steuert die Konvergenz des Algorithmus. Wenn die Fehlermeldung "zu viele Iterationen" angezeigt wird, versuchen Sie, für r einen kleineren Wert zu verwenden.

7. Rufen Sie die Funktion relax auf.

<region id="ID0E2N15" top="1516.8000000000002" left="38.400000000000006" height="25.6" width="204.10333333333335" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="30">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id xml:space="preserve" labels="VARIABLE">F</id>
      <apply>
        <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">relax</id>
        <sequence>
          <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">a</id>
          <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">b</id>
          <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">c</id>
          <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">d</id>
          <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">e</id>
          <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">S</id>
          <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">f</id>
          <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">r</id>
        </sequence>
      </apply>
    </define>
  </math>
</region>

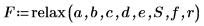
8. Erstellen Sie ein 3D-Diagramm, um die Wärmeverteilung auf der quadratischen Platte darzustellen.

<region id="ID0ELP15" top="1747.2000000000003" left="38.400000000000006" height="301.40000715255735" width="297.6000071525574" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white">
    <plot3D>
      <traces>
        <trace3D resultRef="32" num-of-points="41" SurfaceFill="#00FFFFFF">
          <traceStyle color="#FFED1D2F">surface</traceStyle>
        </trace3D>
      </traces>
      <graph-size width="240.00000715255737" height="240.00000715255737" />
      <axes>
        <xAxis rank="1" start="0" end="32">
          <axisLine />
          <axisGrid>
            <gridFrequency>5</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <numberFormat>
            <general precision="3" />
          </numberFormat>
          <xyDomain auto-scale="true" allow-negative-values="true" scale-type="linear">
            <startValue />
            <endValue />
          </xyDomain>
        </xAxis>
        <yAxis rank="1" start="0" end="32">
          <axisLine />
          <axisGrid>
            <gridFrequency>5</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <numberFormat>
            <general precision="3" />
          </numberFormat>
          <xyDomain auto-scale="true" allow-negative-values="true" scale-type="linear">
            <startValue />
            <endValue />
          </xyDomain>
        </yAxis>
        <zAxis rank="1" start="-3" end="4.5">
          <axisLine />
          <axisGrid>
            <gridFrequency>6</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <numberFormat>
            <general precision="3" />
          </numberFormat>
          <zDomain auto-scale="true" allow-negative-values="true" scale-type="linear">
            <startValue />
            <endValue />
          </zDomain>
        </zAxis>
      </axes>
      <plotEquations>
        <plotEquation>
          <math>
            <apply xmlns="http://schemas.mathsoft.com/math50">
              <neg />
              <id xml:space="preserve">F</id>
            </apply>
          </math>
          <math>
            <placeholder xmlns="http://schemas.mathsoft.com/math50" />
          </math>
        </plotEquation>
      </plotEquations>
      <CameraTransformMatrix Columns="4" Rows="4">
        <Cells>
          <Cell>-0.052623873051966662</Cell>
          <Cell>0.043294250885890617</Cell>
          <Cell>0.99767546618388891</Cell>
          <Cell>0</Cell>
          <Cell>0.095704097834471175</Cell>
          <Cell>0.99467978821191028</Cell>
          <Cell>-0.038116198399097093</Cell>
          <Cell>0</Cell>
          <Cell>-0.99401783366431629</Cell>
          <Cell>0.093475808436936883</Cell>
          <Cell>-0.056487340124674094</Cell>
          <Cell>0</Cell>
          <Cell>0</Cell>
          <Cell>0</Cell>
          <Cell>0</Cell>
          <Cell>1</Cell>
        </Cells>
      </CameraTransformMatrix>
      <CameraType>Orthografisch</CameraType>
    </plot3D>
  </plot>
</region>

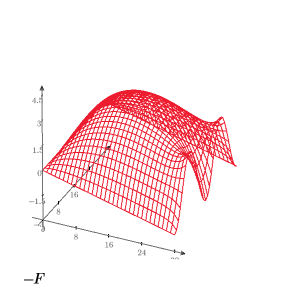
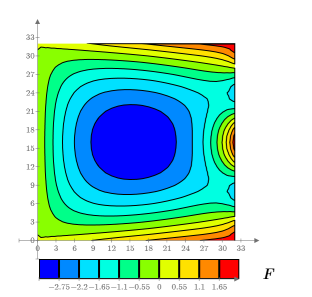
9. Erstellen Sie ein Isolinienplot, um die Linien mit konstanter Temperatur anzuzeigen.

Zugehörige Themen

Relaxationsverfahren für eine partielle Differentialgleichung

War dies hilfreich?