Beispiel: Wärmefluss auf einer quadratischen Platte

Funktionen > Lösen und Optimieren > Lösungsalgorithmen für Differentialgleichungen > Beispiel: Wärmefluss auf einer quadratischen Platte - I

Beispiel: Wärmefluss auf einer quadratischen Platte - I

Lösen Sie die Gleichung für die Beharrungstemperaturverteilung einer quadratischen Platte mit dem Gleichungslöser für partielle Differentialgleichungen multigrid.

Laplace-Gleichungen lösen

Suchen Sie die Temperatur T(x,y) einer quadratischen Platte mit einer konstanten internen Wärmequelle. Die Grenze der Quelle wird bei null Grad festgelegt.

1. Definieren Sie die Bemaßung der quadratischen Platte:

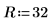
2. Schreiben Sie eine Laplace-Gleichung in zwei Variablen, um Punkte auf der Platte darzustellen, die von der Wärmequelle unabhängig sind:

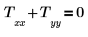
3. Legen Sie die Bemaßungen der Wärmequelle ρ fest:

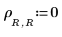
4. Legen Sie die Position der Wärmequelle fest:

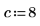
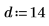
5. Legen Sie die Kraft der Wärmequelle fest:

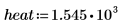
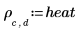
6. Legen Sie die Anzahl der Zyklen auf jeder Stufe der multigrid-Iteration fest:

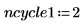
7. Ermitteln Sie die Lösung mithilfe der Funktion multigrid:

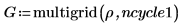
8. Erstellen Sie ein 3D-Diagramm, um die Wärmeverteilung auf der quadratischen Platte darzustellen:

<region id="ID0ETQY5" top="1036.8000000000002" left="38.400000000000006" height="301.40000715255735" width="297.6000071525574" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white">
    <plot3D>
      <traces>
        <trace3D resultRef="56" num-of-points="41" SurfaceFill="#00FFFFFF">
          <traceStyle color="#FFED1D2F">surface</traceStyle>
        </trace3D>
      </traces>
      <graph-size width="240.00000715255737" height="240.00000715255737" />
      <axes>
        <xAxis rank="1" start="0" end="32">
          <axisLine />
          <axisGrid>
            <gridFrequency>5</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <numberFormat>
            <general precision="3" />
          </numberFormat>
          <xyDomain auto-scale="true" allow-negative-values="true" scale-type="linear">
            <startValue />
            <endValue />
          </xyDomain>
        </xAxis>
        <yAxis rank="1" start="0" end="32">
          <axisLine />
          <axisGrid>
            <gridFrequency>5</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <numberFormat>
            <general precision="3" />
          </numberFormat>
          <xyDomain auto-scale="true" allow-negative-values="true" scale-type="linear">
            <startValue />
            <endValue />
          </xyDomain>
        </yAxis>
        <zAxis rank="1" start="0" end="1.25">
          <axisLine />
          <axisGrid>
            <gridFrequency>6</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <numberFormat>
            <general precision="3" />
          </numberFormat>
          <zDomain auto-scale="true" allow-negative-values="true" scale-type="linear">
            <startValue />
            <endValue />
          </zDomain>
        </zAxis>
      </axes>
      <plotEquations>
        <plotEquation>
          <math>
            <apply xmlns="http://schemas.mathsoft.com/math50">
              <neg />
              <id xml:space="preserve">G</id>
            </apply>
          </math>
          <math>
            <placeholder xmlns="http://schemas.mathsoft.com/math50" />
          </math>
        </plotEquation>
      </plotEquations>
      <CameraTransformMatrix Columns="4" Rows="4">
        <Cells>
          <Cell>-0.033544651990996412</Cell>
          <Cell>0.15928240904068555</Cell>
          <Cell>0.98666299742769259</Cell>
          <Cell>0</Cell>
          <Cell>0.30398219843693014</Cell>
          <Cell>0.942073234763303</Cell>
          <Cell>-0.14174922707393303</Cell>
          <Cell>0</Cell>
          <Cell>-0.95208695997595394</Cell>
          <Cell>0.29517305858225334</Cell>
          <Cell>-0.080020535682685218</Cell>
          <Cell>0</Cell>
          <Cell>0</Cell>
          <Cell>0</Cell>
          <Cell>0</Cell>
          <Cell>1</Cell>
        </Cells>
      </CameraTransformMatrix>
      <CameraType>Orthografisch</CameraType>
    </plot3D>
  </plot>
</region>

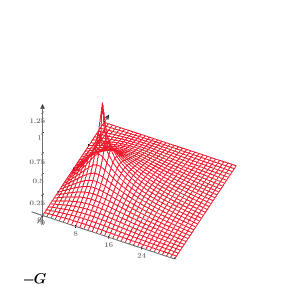
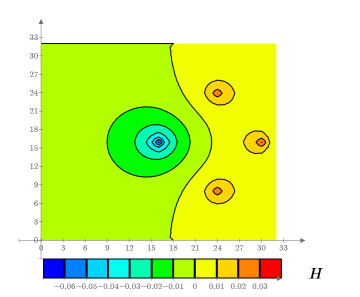
9. Erstellen Sie ein Isolinienplot, um die Linien mit konstanter Temperatur anzuzeigen:

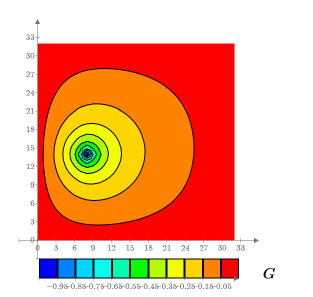
10. Definieren Sie eine andere Konfiguration von Wärmequellen, die andere Positionen aufweisen:

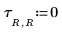
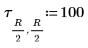
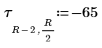
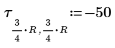
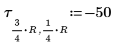
11. Legen Sie die Anzahl der Zyklen auf jeder Stufe der multigrid-Iteration fest:

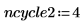
12. Ermitteln Sie die Lösung mithilfe der Funktion multigrid:

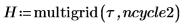
13. Erstellen Sie ein 3D-Diagramm, um die Wärmeverteilung auf der quadratischen Platte darzustellen:

<region id="ID0ED1Y5" top="2265.6000000000004" left="38.400000000000006" height="301.40000715255735" width="297.6000071525574" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white">
    <plot3D>
      <traces>
        <trace3D resultRef="76" num-of-points="41" SurfaceFill="#00FFFFFF">
          <traceStyle color="#FF2E3192">surface</traceStyle>
        </trace3D>
      </traces>
      <graph-size width="240.00000715255737" height="240.00000715255737" />
      <axes>
        <xAxis rank="1" start="0" end="32">
          <axisLine />
          <axisGrid>
            <gridFrequency>5</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <numberFormat>
            <general precision="3" />
          </numberFormat>
          <xyDomain auto-scale="true" allow-negative-values="true" scale-type="linear">
            <startValue />
            <endValue />
          </xyDomain>
        </xAxis>
        <yAxis rank="1" start="0" end="32">
          <axisLine />
          <axisGrid>
            <gridFrequency>5</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <numberFormat>
            <general precision="3" />
          </numberFormat>
          <xyDomain auto-scale="true" allow-negative-values="true" scale-type="linear">
            <startValue />
            <endValue />
          </xyDomain>
        </yAxis>
        <zAxis rank="1" start="-0.09" end="0.06">
          <axisLine />
          <axisGrid>
            <gridFrequency>6</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <numberFormat>
            <general precision="3" />
          </numberFormat>
          <zDomain auto-scale="true" allow-negative-values="true" scale-type="linear">
            <startValue />
            <endValue />
          </zDomain>
        </zAxis>
      </axes>
      <plotEquations>
        <plotEquation>
          <math>
            <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">H</id>
          </math>
          <math>
            <placeholder xmlns="http://schemas.mathsoft.com/math50" />
          </math>
        </plotEquation>
      </plotEquations>
      <CameraTransformMatrix Columns="4" Rows="4">
        <Cells>
          <Cell>0.28776910670726691</Cell>
          <Cell>0.14277686867570288</Cell>
          <Cell>-0.94699720537922527</Cell>
          <Cell>0</Cell>
          <Cell>-0.33031167875973361</Cell>
          <Cell>0.942946222767463</Cell>
          <Cell>0.04179253334628906</Cell>
          <Cell>0</Cell>
          <Cell>0.89893444482889184</Cell>
          <Cell>0.30077763670149293</Cell>
          <Cell>0.31851165937911374</Cell>
          <Cell>0</Cell>
          <Cell>0</Cell>
          <Cell>0</Cell>
          <Cell>0</Cell>
          <Cell>1</Cell>
        </Cells>
      </CameraTransformMatrix>
      <CameraType>Orthografisch</CameraType>
    </plot3D>
  </plot>
</region>

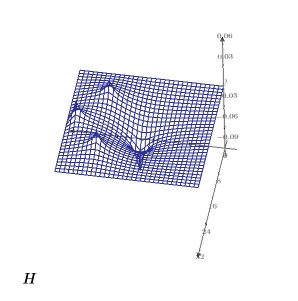
14. Erstellen Sie ein Isolinienplot, um die Linien mit konstanter Temperatur anzuzeigen:

Zugehörige Themen

Relaxationsverfahren für eine partielle Differentialgleichung

War dies hilfreich?