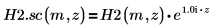Beispiel: Hankel-Funktionen der ersten und zweiten Art

Funktionen > Spezielle Funktionen > Bessel-Funktionen > Beispiel: Hankel-Funktionen der ersten und zweiten Art

Zeigen Sie die Beziehung zwischen den Hankel-Funktionen H1 und H2 mit den Bessel-Funktionen Jn und Yn an. Zeigen Sie auch die Beziehungen zwischen diesen Funktionen und ihren skalierten Versionen an.

Die Hankel-Funktionen sind bei 0 nicht definiert.

1. Verwenden Sie die symbolische Auswertung, um die Beziehung zwischen H1, Jn und Yn anzuzeigen.

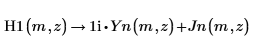
2. Verwenden Sie die symbolische Auswertung, um die Beziehung zwischen H2, Jn und Yn anzuzeigen.

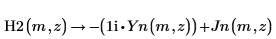
◦ Die reellen Komponenten von H1 und H2 sind in Bezug auf den Wert und das Vorzeichen identisch.

◦ Die imaginären Komponenten von H1 und H2 sind in Bezug auf den Wert und das Vorzeichen identisch.

3. Beachten Sie auch die beiden folgenden wichtigen Beziehungen zwischen H1 und H2.

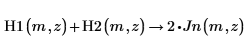
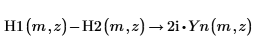
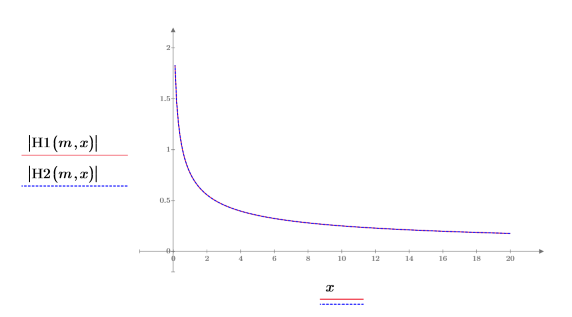
4. Erstellen Sie ein Diagramm, um zu zeigen, dass |H1|=|H2|.

<region id="ID0EZ6Y6" actualWidth="571.66857242138985" actualHeight="316.8" top="192.00000000000003" left="0" height="316.8" width="571.66857242138985" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="33">
          <traceStyle color="#FFED1D2F" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
        <trace resultRef="34">
          <traceStyle color="#FF0000FF" symbol="none" line-weight="1" line-style="Dash">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="418.06857242139" height="259.2" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="0" end="20">
          <axisLine position="origin" positionticmark="0" legendWidth="60.93" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <plotEquations>
            <plotEquation>
              <math>
                <id labels="VARIABLE" label-is-contextual="true" xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">x</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="0" end="2">
          <axisLine position="origin" positionticmark="0" legendWidth="125.873333333333" />
          <axisGrid>
            <gridFrequency>5</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <plotEquations>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <absval />
                  <apply>
                    <id labels="FUNCTION" xml:space="preserve">H1</id>
                    <sequence>
                      <id labels="VARIABLE" label-is-contextual="true" xml:space="preserve">m</id>
                      <id labels="VARIABLE" label-is-contextual="true" xml:space="preserve">x</id>
                    </sequence>
                  </apply>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <absval />
                  <apply>
                    <id labels="FUNCTION" label-is-contextual="true" xml:space="preserve">H2</id>
                    <sequence>
                      <id labels="VARIABLE" label-is-contextual="true" xml:space="preserve">m</id>
                      <id labels="VARIABLE" label-is-contextual="true" xml:space="preserve">x</id>
                    </sequence>
                  </apply>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="35">
              <real xmlns="http://schemas.mathsoft.com/math50">0</real>
            </startValue>
            <secondTickValue resultRef="36">
              <real xmlns="http://schemas.mathsoft.com/math50">0.5</real>
            </secondTickValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

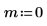
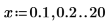
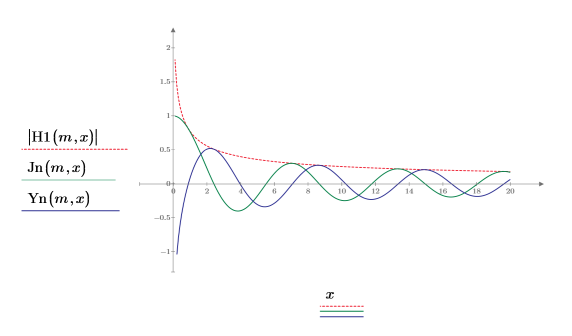
5. Erstellen Sie ein Diagramm, um die Beziehung zwischen H1, Jn und Yn zu zeigen.

<region id="ID0EVBZ6" actualWidth="571.66857242139008" actualHeight="336" top="518.40000000000009" left="0" height="336" width="571.66857242139008" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="37">
          <traceStyle color="#FFED1D2F" symbol="none" line-weight="1" line-style="Dash">Linien</traceStyle>
        </trace>
        <trace resultRef="38">
          <traceStyle color="#FF068149" symbol="none" line-weight="1" line-style="Solid">Linien</traceStyle>
        </trace>
        <trace resultRef="39">
          <traceStyle color="#FF2E3192" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="418.06857242139" height="259.2" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="0" end="20">
          <axisLine position="origin" positionticmark="2" legendWidth="60.93" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <plotEquations>
            <plotEquation>
              <math>
                <id labels="VARIABLE" label-is-contextual="true" xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">x</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="-1" end="2">
          <axisLine position="origin" positionticmark="0" legendWidth="125.873333333333" />
          <axisGrid>
            <gridFrequency>7</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <plotEquations>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <absval />
                  <apply>
                    <id labels="FUNCTION" xml:space="preserve">H1</id>
                    <sequence>
                      <id labels="VARIABLE" label-is-contextual="true" xml:space="preserve">m</id>
                      <id labels="VARIABLE" label-is-contextual="true" xml:space="preserve">x</id>
                    </sequence>
                  </apply>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <id labels="FUNCTION" xml:space="preserve">Jn</id>
                  <sequence>
                    <id labels="VARIABLE" label-is-contextual="true" xml:space="preserve">m</id>
                    <id labels="VARIABLE" label-is-contextual="true" xml:space="preserve">x</id>
                  </sequence>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <id labels="FUNCTION" label-is-contextual="true" xml:space="preserve">Yn</id>
                  <sequence>
                    <id labels="VARIABLE" label-is-contextual="true" xml:space="preserve">m</id>
                    <id labels="VARIABLE" label-is-contextual="true" xml:space="preserve">x</id>
                  </sequence>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="40">
              <real xmlns="http://schemas.mathsoft.com/math50">-1</real>
            </startValue>
            <secondTickValue resultRef="41">
              <real xmlns="http://schemas.mathsoft.com/math50">-0.5</real>
            </secondTickValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

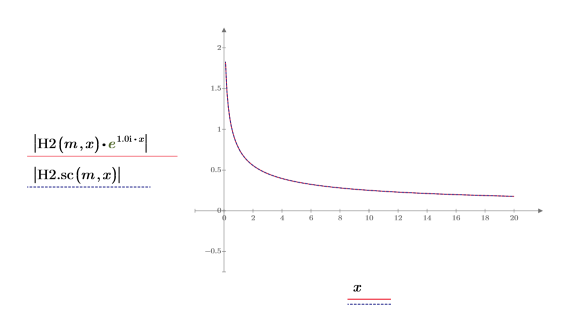
6. Verwenden Sie die symbolische Auswertung, um die Beziehung zwischen den Hankel-Funktionen und ihrer skalierten Version zu zeigen.

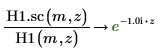
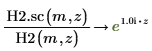
7. Erstellen Sie ein Diagramm, um Folgendes zu zeigen:

<region id="ID0ERFZ6" actualWidth="571.2685724213901" actualHeight="316.8" top="1017.6000000000001" left="0" height="316.8" width="571.2685724213901" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="45">
          <traceStyle color="#FFED1D2F" symbol="none" line-weight="1" line-style="Solid">Linien</traceStyle>
        </trace>
        <trace resultRef="46">
          <traceStyle color="#FF2E3192" symbol="none" line-weight="1" line-style="Dash">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="360.06857242139" height="259.2" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="0" end="20">
          <axisLine position="origin" positionticmark="1" legendWidth="60.93" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <plotEquations>
            <plotEquation>
              <math>
                <id labels="VARIABLE" label-is-contextual="true" xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">x</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="-0.5" end="2">
          <axisLine position="origin" positionticmark="0" legendWidth="178.54" />
          <axisGrid>
            <gridFrequency>6</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <plotEquations>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <absval />
                  <apply>
                    <mult />
                    <apply>
                      <id labels="FUNCTION" xml:space="preserve">H1</id>
                      <sequence>
                        <id labels="VARIABLE" label-is-contextual="true" xml:space="preserve">m</id>
                        <id labels="VARIABLE" label-is-contextual="true" xml:space="preserve">x</id>
                      </sequence>
                    </apply>
                    <apply>
                      <pow />
                      <id labels="CONSTANT" label-is-contextual="true" xml:space="preserve">e</id>
                      <apply>
                        <mult />
                        <imag symbol="i">-1.0</imag>
                        <id labels="VARIABLE" label-is-contextual="true" xml:space="preserve">x</id>
                      </apply>
                    </apply>
                  </apply>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <absval />
                  <apply>
                    <id labels="FUNCTION" label-is-contextual="true" xml:space="preserve">H1.sc</id>
                    <sequence>
                      <id labels="VARIABLE" label-is-contextual="true" xml:space="preserve">m</id>
                      <id labels="VARIABLE" label-is-contextual="true" xml:space="preserve">x</id>
                    </sequence>
                  </apply>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="47">
              <real xmlns="http://schemas.mathsoft.com/math50">-0.5</real>
            </startValue>
            <secondTickValue resultRef="48">
              <real xmlns="http://schemas.mathsoft.com/math50">0</real>
            </secondTickValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

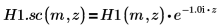
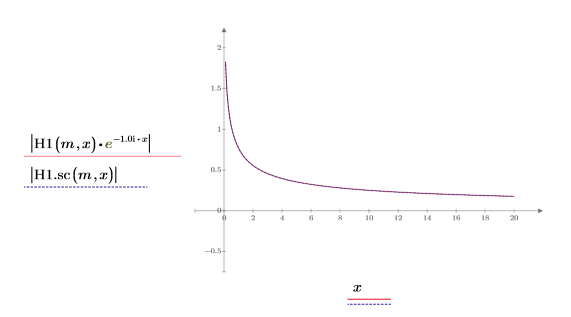
8. Erstellen Sie ein Diagramm, um Folgendes zu zeigen:

<region id="ID0EPHZ6" actualWidth="571.26857242139" actualHeight="316.8" top="1382.4" left="0" height="316.8" width="571.26857242139" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="50">
          <traceStyle color="#FFED1D2F" symbol="none" line-weight="1" line-style="Solid">Linien</traceStyle>
        </trace>
        <trace resultRef="51">
          <traceStyle color="#FF2E3192" symbol="none" line-weight="1" line-style="Dash">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="360.06857242139" height="259.2" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="0" end="20">
          <axisLine position="origin" positionticmark="1" legendWidth="60.93" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <plotEquations>
            <plotEquation>
              <math>
                <id labels="VARIABLE" label-is-contextual="true" xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">x</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="-0.5" end="2">
          <axisLine position="origin" positionticmark="0" legendWidth="171.7" />
          <axisGrid>
            <gridFrequency>6</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <plotEquations>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <absval />
                  <apply>
                    <mult />
                    <apply>
                      <id labels="FUNCTION" xml:space="preserve">H2</id>
                      <sequence>
                        <id labels="VARIABLE" label-is-contextual="true" xml:space="preserve">m</id>
                        <id labels="VARIABLE" label-is-contextual="true" xml:space="preserve">x</id>
                      </sequence>
                    </apply>
                    <apply>
                      <pow />
                      <id labels="CONSTANT" label-is-contextual="true" xml:space="preserve">e</id>
                      <apply>
                        <mult />
                        <imag symbol="i">1.0</imag>
                        <id labels="VARIABLE" label-is-contextual="true" xml:space="preserve">x</id>
                      </apply>
                    </apply>
                  </apply>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <absval />
                  <apply>
                    <id labels="FUNCTION" label-is-contextual="true" xml:space="preserve">H2.sc</id>
                    <sequence>
                      <id labels="VARIABLE" label-is-contextual="true" xml:space="preserve">m</id>
                      <id labels="VARIABLE" label-is-contextual="true" xml:space="preserve">x</id>
                    </sequence>
                  </apply>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="52">
              <real xmlns="http://schemas.mathsoft.com/math50">-0.5</real>
            </startValue>
            <secondTickValue resultRef="53">
              <real xmlns="http://schemas.mathsoft.com/math50">0</real>
            </secondTickValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

Zugehörige Themen

Hankel-Funktionen

War dies hilfreich?