Beispiel: Fourier-Polynom
1. Schreiben Sie ein Programm, das eine periodische Funktion generiert:
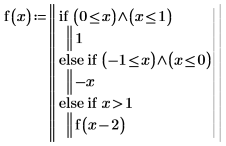
2. Stellen Sie Funktion grafisch dar:
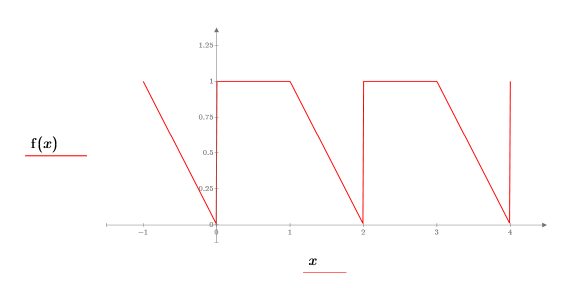
3. Geben Sie den positiven Endpunkt des periodischen Intervalls ein:
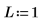
4. Geben Sie die Reihenfolge der Fourier-Reihen-Approximation an:
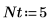
5. Schreiben Sie ein Programm zum Berechnen der Fourier-Koeffizienten:
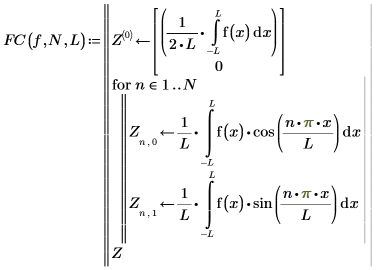
6. Berechnen Sie die Fourier-Koeffizienten:
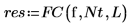
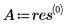
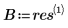
7. Berechnen Sie das n-te Fourier-Polynom:
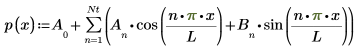
8. Stellen Sie das Fourier-Polynom und die ursprüngliche Funktion grafisch dar:
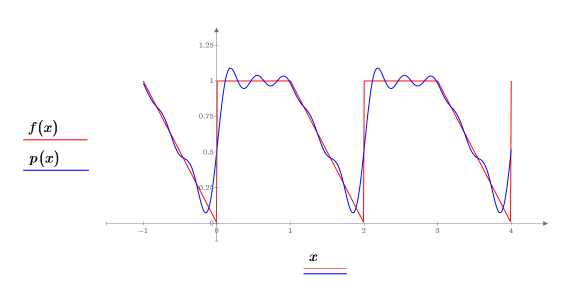
Die Näherung P1 von f ist mangelhaft in der Nähe der Hochfrequenzpunkte (der scharfen Kanten).
9. Berechnen Sie die Fourier-Koeffizienten:
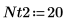
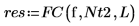
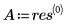
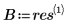
10. Berechnen Sie das n-te Fourier-Polynom:
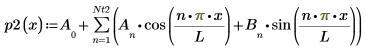
11. Stellen Sie das Fourier-Polynom und die ursprüngliche Funktion grafisch dar:
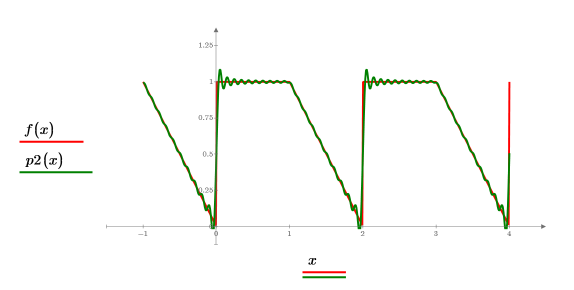
Die Näherung P2, die Nt=20 verwendet, ist eine wesentlich bessere Näherung der ursprünglichen Funktion, insbesondere an den Hochfrequenzpunkten (den scharfen Kanten).