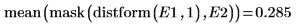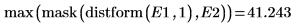Beispiel: Euklidische Abstandstransformation
Verwenden Sie die Funktion distform, um die euklidische Abstandstransformation von Matrix M zu berechnen, wobei Pixel mit dem Wert fg als Vordergrund-Pixel berücksichtigt werden.
Weitere Informationen zur Verwendung dieses Beispiels finden Sie unter Bildverarbeitungsbeispiele.
Bildmatrix
1. Definieren Sie eine Bildmatrix, und wenden Sie distform darauf an.
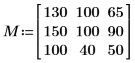
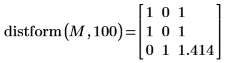
Der Wert jedes Ausgabepixels entspricht dem Abstand zum nächstgelegenen eingegebenen Vordergrundpixel (Wert 100):
◦ Für eingegebene Vordergrundpixel weist der ausgegebene Abstand den Wert null auf.
◦ Für horizontale und vertikale Nachbarn weist der Abstand den Wert 1 auf.
◦ Für diagonale Nachbarn ist der Abstand die Quadratwurzel 2 oder 1.414.
Bild mit einem einzigen Pixel ungleich null
1. Definieren Sie ein Bild mit einem einzigen Pixel ungleich null.
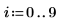
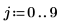
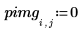
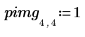

2. Wenden Sie distform auf das Bild an:
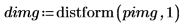
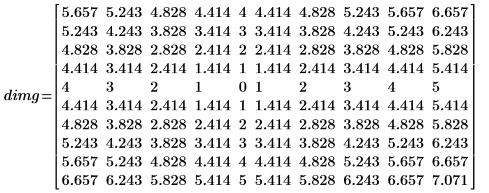
Der Abstand erhöht sich auf monotone Weise, während Sie sich von dem Vordergrundpixel (dem Mittelpixel) in dem Eingabebild entfernen.
Die Abstandstransformation produziert einen ungefähren euklidischen Abstand. In dem Beispiel oben können Sie sehen, dass die genaue Ausgabe der euklidischen Abstandstransformation für die Matrixposition (0,1) folgendermaßen lauten sollte:
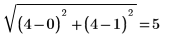
wobei der Wert in unserem Ausgabebild 5.243 lautet.
Bild eines kreisförmigen Objekts
1. Definieren Sie ein Bild eines Kreises:
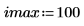
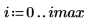
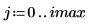
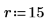
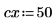
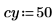
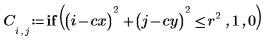
2. Verwenden Sie die Funktion scale, um den Kreis zu skalieren.
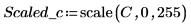
3. Verwenden Sie die Funktion WRITEBMP, um den skalierten Kreis in eine Datei zu schreiben.
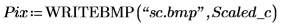
4. Wenden Sie die Funktion distform auf den Kreis an, skalieren Sie ihn, und speichern Sie die Ergebnisse in einer neuen Datei.
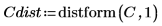
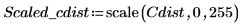
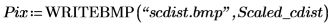
5. Fügen Sie die Bilder aus den beiden Dateien ein, und vergleichen Sie das Ergebnis.
 |  |
(sc.bmp) | (scdist.bmp) |
Die Abstandswerte lauten null für alle Punkte im Kreis und erhöhen sich auf monotone Weise, während Sie sich nach außen bewegen. Sie entsprechen jedoch nicht exakt dem euklidischen Abstand. Ansonsten wäre die Ausgabe radialsymmetrisch.
Zwei binäre Bilder eines einzelnen Objekts
1. Lesen Sie ein Bild ein.
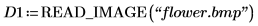
2. Verwenden Sie die Funktion translate, um verschobene Versionen des Bildes zu erstellen und die verschobenen Bilder in Dateien zu schreiben.
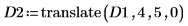
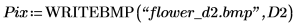
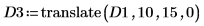
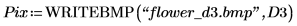
3. Fügen Sie die Bilder aus den drei Dateien ein, und vergleichen Sie das Ergebnis.
 |  |  |
(flower.bmp) | (flower_d2.bmp) | (flower_d3.bmp) |
4. Verwenden Sie die Funktion distform, um die Abstandtransformation von D1 zu berechnen.
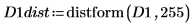
5. Verwenden Sie die Funktionen mask und mean, um das Abstandstransformationsbild mit den Bildern D2 und D3 zu maskieren und den Mittelwert des gesamten Bildes zu berechnen. Dies entspricht einer Messung des Abstands zwischen den beiden Bildern.
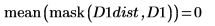
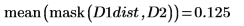
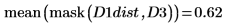
Der Abstand zwischen D1 und D1 weist den Wert null auf, und der Abstand zwischen D1 und den anderen Bildern erhöht sich mit dem Translationsgrad.
6. Berechnen Sie den Hausdorff-Abstand
Der Hausdorff-Abstand ist als Maximalwert des kürzesten Abstands zwischen Punkten in zwei Sätzen definiert. Um den Hausdorff-Abstand zwischen den beiden Bildern zu berechnen, verwenden Sie die Funktion max anstelle der Funktion mean.
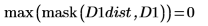
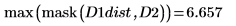
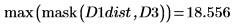
Bilder mit zwei Kanten
Sie können die Leistung von Kantendetektoren vergleichen, indem Sie den Abstand zwischen Bildern mit zwei Kanten berechnen. Verwenden Sie entweder den Mittelwert oder den Maximalwert der maskierten Abstände als Messgröße für den Kantenabstand.
1. Verwenden Sie die Funktion READ_IMAGE, um eine Bilddatei zu lesen.
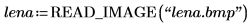
2. Wenden Sie die beiden Kantendetektoren canny und binarize auf das Bild an, und schreiben Sie die Ergebnisse in externe Dateien.
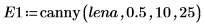
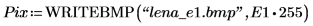
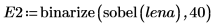
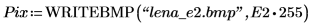
3. Fügen Sie die beiden Bilder ein, und vergleichen Sie sie visuell.
 |  |
(lena_e1.bmp) | (lena_e2.bmp) |
4. Berechnen Sie den gesamten Abstand zwischen den Kanten.