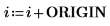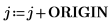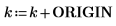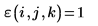Beispiel: Wirkung von ORIGIN auf Nicht-Suchfunktionen
Die Systemvariable ORIGIN wirkt sich auf das Ergebnis von drei Funktionen aus, die Arrays verarbeiten: submatrix, csort und rsort.
Sie wirkt sich auch auf eine Funktion aus, die keine Arrays verarbeitet: e (die antisymmetrische Tensorfunktion).
1. Definieren Sie eine Eingabematrix.

2. Werten Sie ORIGIN aus, um sicherzustellen, dass die Variable auf 0 festgelegt ist.
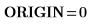
ORIGIN=0: submatrix, csort und rsort
1. Legen Sie die Zeilen- und Spaltenargumente fest.
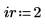
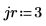
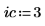
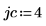
2. Verwenden Sie die Funktion submatrix, um eine Submatrix aus der Matrix M zu extrahieren.
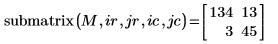
Das Ergebnis ist die Submatrix, die sich zwischen den Zeilen 2 und 3 und den Spalten 3 und 4 befindet.
3. Legen Sie das Spaltenargument fest, und werten Sie die Spaltensortenfunktion csort aus.
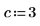

Die zurückgegebene Matrix ist das Ergebnis der Neuanordnung der Zeilen von M, bis sich Spalte 3 in aufsteigender Reihenfolge befindet
4. Legen Sie das Zeilenargument fest, und werten Sie die Zeilensortenfunktion rsort aus.
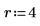

Die zurückgegebene Matrix ist das Ergebnis der Neuanordnung der Spalten von M, bis sich Zeile 4 in aufsteigender Reihenfolge befindet.
ORIGIN=1: submatrix, csort und rsort
1. Legen Sie ORIGIN auf 1 fest.
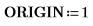
2. Werten Sie die Funktion submatrix erneut aus.
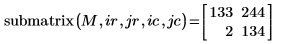
Die zurückgegebene Matrix ergibt sich jetzt aus den Zeilen 1 und 2 und den Spalten 2 und 3.
3. Zeigen Sie Folgendes: Um dieselben Ergebnisse zu erhalten, wenn ORIGIN auf 0 festgelegt ist, müssen Sie den neuen Wert von ORIGIN den Zeilen- und Spaltenindizes der Funktion submatrix hinzufügen.
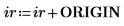
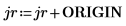
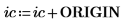
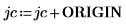
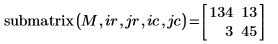
4. Werten Sie die Funktion csort erneut aus.

Die zurückgegebene Matrix zeigt, dass jetzt Spalte 2 (nicht Spalte 3) in aufsteigender Reihenfolge sortiert ist.
5. Zeigen Sie Folgendes: Um dieselben Ergebnisse zu erhalten, wenn ORIGIN auf 0 festgelegt ist, müssen Sie den neuen Wert von ORIGIN dem Argument c hinzufügen.
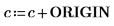

6. Werten Sie die Funktion rsort erneut aus.

Die zurückgegebene Matrix zeigt, dass jetzt Zeile 3 (nicht Zeile 4) in aufsteigender Reihenfolge sortiert ist.
7. Zeigen Sie Folgendes: Um dieselben Ergebnisse zu erhalten, wenn ORIGIN auf 0 festgelegt ist, müssen Sie den neuen Wert von ORIGIN dem Argument r hinzufügen.
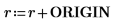

ORIGIN=0: e
1. Legen Sie ORIGIN auf 0 fest.
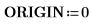
2. Legen Sie die drei Argumente der antisymmetrischen Tensorfunktion fest: i, j und k.
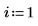
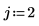
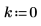
3. Werten Sie die antisymmetrische Tensorfunktion ε aus.
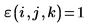
ORIGIN=1: e
1. Legen Sie ORIGIN auf 1 fest.
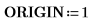
2. Werten Sie die antisymmetrische Tensorfunktion erneut aus.
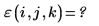
Der Fehler tritt auf, weil jedes Argument einen Wert zwischen ORIGIN und ORIGIN+2 haben muss.
3. Zeigen Sie Folgendes: Um dieselben Ergebnisse zu erhalten, wenn ORIGIN auf 0 festgelegt ist, müssen Sie den neuen Wert von ORIGIN jedem der drei Argumente hinzufügen.