Beispiel: Ausdünnen eines Vektors

Funktionen > Vektor und Matrix > Array-Eigenschaften > Beispiel: Ausdünnen eines Vektors

Verwenden Sie die folgende Methode, um jedes n-te Element aus einem Datenvektor auszuwählen und dabei mit dem ersten Element zu beginnen. Dies zeigt die Auswirkungen von überhöhtem Ausdünnen (Nyquist-Theorem).

1. Definieren Sie die Periode und die Abtastfrequenz.

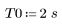
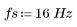
2. Erstellen Sie einen Signalvektor.

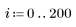
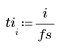
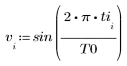
3. Definieren Sie eine Ganzzahl n, die kleiner als die Länge von Vektor v ist.

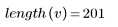
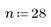
4. Verwenden Sie die Vektorindizierung zum Extrahieren jedes n-ten Elements von Vektor v.

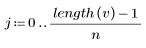
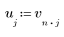
5. Stellen Sie die ursprüngliche und die ausgedünnte Spur grafisch dar.

<region id="ID0EBA5EB" top="864" left="24" width="598" height="312" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot origin-positioning="false">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace>
          <traceStyle color="#FF00008B" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
        <trace>
          <traceStyle color="#FFFF0000" symbol="x" line-weight="1" line-style="Dash">lines</traceStyle>
        </trace>
      </traces>
      <axes>
        <xAxis legend-position="PlotBoundaryBottom" rank="1">
          <axisLine position="origin" positionticmark="5" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat />
          <plotEquations>
            <plotEquation>
              <math>
                <id xmlns="http://schemas.mathsoft.com/math50">range1</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <id xmlns="http://schemas.mathsoft.com/math50">range2</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <real xmlns="http://schemas.mathsoft.com/math50">0</real>
            </startValue>
            <endValue>
              <real xmlns="http://schemas.mathsoft.com/math50">200</real>
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis legend-position="PlotBoundaryLeft" rank="1">
          <axisLine position="ticknumberlock" positionticmark="5" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat />
          <plotEquations>
            <plotEquation>
              <math>
                <id xmlns="http://schemas.mathsoft.com/math50">v</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <id xmlns="http://schemas.mathsoft.com/math50">u</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <real xmlns="http://schemas.mathsoft.com/math50">-1</real>
            </startValue>
            <endValue>
              <real xmlns="http://schemas.mathsoft.com/math50">1</real>
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

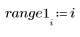
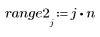
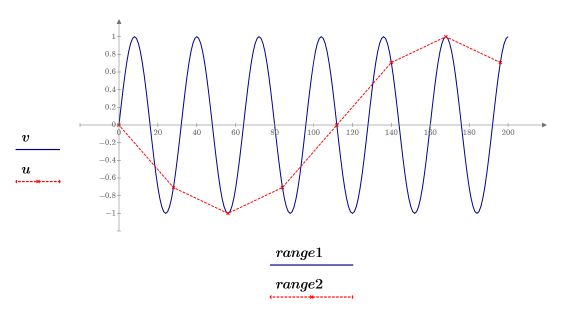
◦ Falls die neue Abtastrate zu langsam ist (zu große Abstände), kann das Signal sehr verzerrt aussehen (versuchen Sie n = 15), vollständig verschwinden (nur die 0-Punkte werden abgetastet - versuchen Sie n = 16), oder es kann Aliasing auftreten, d.h., das Signal kann eine falsche Frequenz aufweisen (n = 28, siehe Abbildung), da es nicht genügend Abtastungen gibt, um die Informationen im Signal genau darzustellen.

◦ Das Abtasten weist Konsequenzen für jeden numerischen Algorithmus auf, der ein Ergebnis in diskreten Intervallen annähert (z.B. die Fourier-Transformation und Differentialgleichungslöser).

◦ Um ein Signal sauber ohne Aliasing auszudünnen, muss es einen Tiefpassfilter durchlaufen, der p/n vor dem Entfernen jedes n-ten Punkts abschneidet. Für weitere Informationen, siehe Oppenheim und Schafer, Discrete Time Signal Processing, Prentice Hall, pp 102-105, ©1989.

Zugehörige Themen

Anzahl der Elemente in einem Vektor

War dies hilfreich?