Beispiel: Diskrete Kosinustransformation

Funktionen > Bildverarbeitung > Transformationsbereich > Beispiel: Diskrete Kosinustransformation

Verwenden Sie die Funktionen dct und idct, um die diskrete Kosinustransformation bzw. die inverse Transformation zu berechnen. Diese Transformation hat den Vorteil, dass sie den größten Teil der Bild-"Energie" bzw. der Bildinformationen in ein paar wenige Frequenzkomponenten konzentriert und damit eine gute Auswahl für die Kodierung bildet.

Weitere Informationen zur Verwendung dieses Beispiels finden Sie unter Bildverarbeitungsbeispiele.

1. Definieren Sie eine Matrix M der Größe N x P.

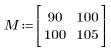
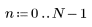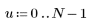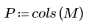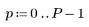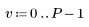2. Die Implementierung der Kosinustransformation verwendet den Typ II DCT. Definieren Sie DCT als eine analytische Formel für diese Transformation.

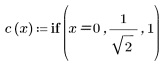
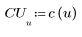
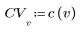
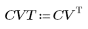
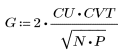
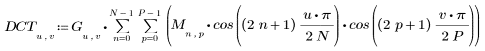
3. Bewerten Sie die Matrix DCT.

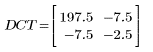
4. Wenden Sie die Funktion dct auf die Matrix M an.

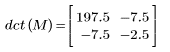
5. Berechnen Sie den maximalen Fehler zwischen DCT und der Funktion dct.

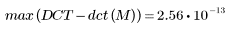
Energieverdichtung

Die Kosinustransformation weist sehr gute Eigenschaften für die Energieverdichtung auf. Dies bedeutet, dass sie den größten Teil der Energie in den ersten Koeffizienten der Transformation konzentriert.

1. Definieren Sie eine Eingabematrix.

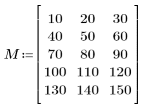
2. Wenden Sie die Funktion dct auf die Matrix M an, und bewerten Sie sie.

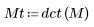
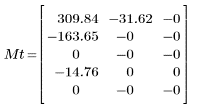
Die resultierende Matrix zeigt, dass der größte Teil der Energie, der sich auf die Koeffizientenwerte bezieht, in den ersten Elementen konzentriert ist.

idct

Die Umkehrfunktion wird verwendet, um das ursprüngliche Bild aus der Transformation wiederherzustellen.

1. Lesen Sie eine Schwarzweißversion des Gemäldes der Mona Lisa ein.

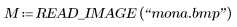
(mona.bmp)

2. Wenden Sie die Funktion dct an, um das Bild zu transformieren.

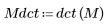
(mona_noise.bmp)

3. Wenden Sie die Umkehrfunktion an, um das ursprüngliche Bild wiederherzustellen.

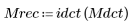
(mona_rec.bmp)

4. Prüfen Sie die Energieverdichtungseigenschaft der diskreten Kosinustransformation (DCT), indem Sie Histogramme des transformierten und des ursprünglichen Bildes anzeigen.

<region id="ID0EL5HZ" top="3000" left="24" width="597" height="312" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace>
          <traceStyle color="#FFFF0000" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
        <trace>
          <traceStyle color="#FF0000FF" symbol="none" line-weight="1" line-style="Solid">columns</traceStyle>
        </trace>
      </traces>
      <axes>
        <xAxis legend-position="PlotBoundaryBottom" rank="1">
          <axisLine position="origin" positionticmark="0" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math>
                <id xmlns="http://schemas.mathsoft.com/math50">k_range</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis legend-position="PlotBoundaryLeft" rank="1">
          <axisLine position="origin" positionticmark="0" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math>
                <id xmlns="http://schemas.mathsoft.com/math50">H</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <id xmlns="http://schemas.mathsoft.com/math50">Horig</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

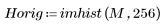
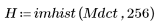
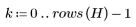
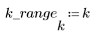
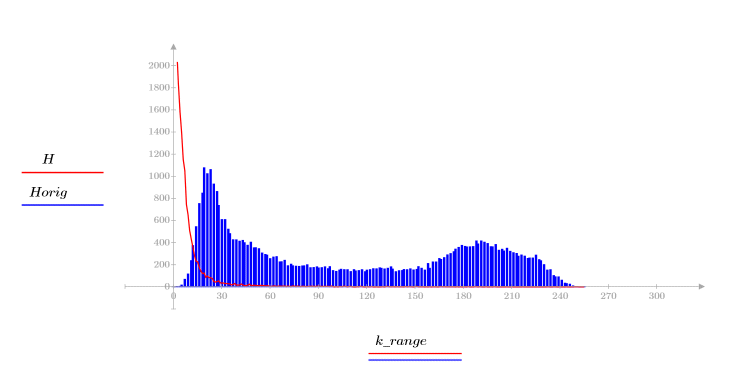
In dem transformierten Bild konzentriert sich die meiste Energie in den ersten Bins des Histogramms, während sie im ursprünglichen Bild verteilt ist. Dadurch ist das transformierte Bild besser für die Kodierung oder Übertragung geeignet, da die meisten Bildinformationen mit sehr wenigen Frequenzkomponenten weitergegeben werden können. Aus diesem Grund wird die diskrete Kosinustransformation (DCT) für Bildkomprimierungen verwendet.

Zugehörige Themen

Diskrete Kosinustransformation

1D- und 2D-Histogramme

War dies hilfreich?