Beispiel: Gedämpfte harmonische Schwingung in Schaltkreisen
Gegeben sei ein einfacher elektrischer Schaltkreis, der einen Widerstand R, einen Induktor L und einen Kondensator C enthält.

Verwenden Sie Differentialgleichungen, um die Ladung Q am Kondensator C zu modellieren, suchen Sie dann mit den GDGL-Gleichungslöserfunktionen andere Näherungslösungen. Vergleichen Sie schließlich die Ergebnisse mit der genauen Lösung von Q.
Differentialgleichungen verwenden
1. Schreiben Sie eine Differentialgleichung für die Spannung an den drei Komponenten, die null betragen muss:
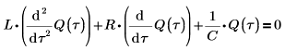
2. Schreiben Sie die Differentialgleichung für die momentane Änderung der Ladung Q von Kondensator C:
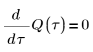
3. Definieren Sie die Ladung Q zum Zeitpunkt null:
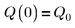
4. Gehen Sie von den folgenden Eingabeparameterwerten aus:
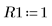
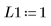
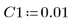
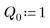
5. Wandeln Sie die Differentialgleichung in die Standardform um:
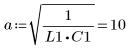
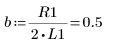
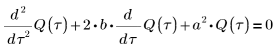
6. Lösen Sie die Gleichung für alle Fällen von a und b:
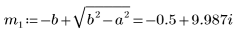
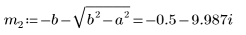
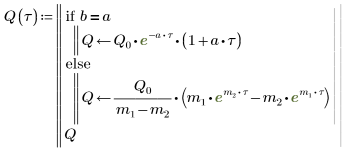
7. Plotten Sie die beiden möglichen Lösungen für Q:
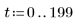
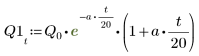
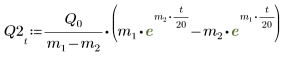
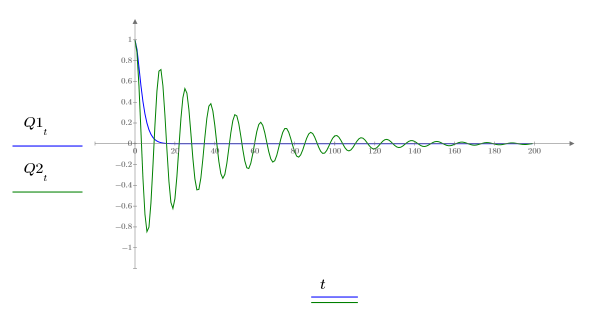
Ladung Q1 fällt schnell auf null (0) ab, wenn a=b, und oszilliert längere Zeit vor dem Erreichen des Nullwerts, wenn a und b ungleich sind.
Vor der Verwendung von GDGL-Gleichungslösern
• Definieren Sie die Parameter, die den Funktionen der GDG-Löser übergeben werden:
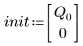 | 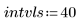 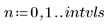 |
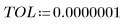 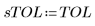 | 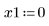 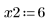 |
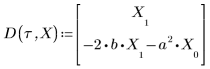 |
• Bei den GDG-Lösern lassen sich zwei Kategorien unterscheiden: Löser für steife Systeme und Löser für nicht-steife Systeme. Ein System aus GDGL, das in Matrixform als y' = Ax dargestellt ist, wird steif genannt, wenn die Matrix A nahezu singulär ist. Andernfalls ist das System nicht-steif.
• Die Unterscheidung zwischen steifen und nicht-steifen Systemen bezieht sich auf die inhärente Dynamikstaffelung von Matrix A, die durch ihre Eigenwerte charakterisiert wird. Eine Matrix mit disparaten Eigenwerten (oder Werten, die von zu klein bis zu groß reichen) ist im Allgemeinen ein steifes System.
• Auf Grundlage der angegebenen Systemparameter stellt dieses einfache Beispiel für gedämpfte harmonische Schwingungen ein nicht-steifes System dar.
• Den Funktionen Adams, AdamsBDF, BDF und Radau kann ein bestimmter TOL-Wert übergeben werden, oder die Funktionen verwenden ihren eigenen TOL-Standardwert von 10-5.
GDGL-Löser für nicht-steife Systeme verwenden
Verwenden Sie die GDGL-Löser für nicht-steife Systeme, um die Näherungslösungen zu finden, und vergleichen Sie anschließend die Ergebnisse mit der genauen Lösung von Q.
1. Adams
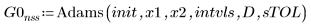
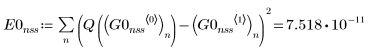
2. rkfixed
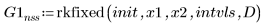
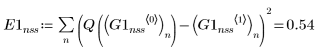
3. Rkadapt
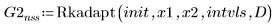
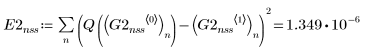
4. Bulstoer
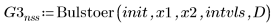
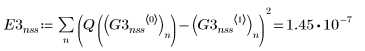
GDGL-Löser für steife Systeme verwenden
Verwenden Sie die GDGL-Löser für steife Systeme, um die Näherungslösungen zu finden, und vergleichen Sie anschließend die Ergebnisse mit der genauen Lösung von Q.
1. BDF
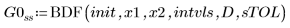
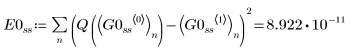
2. Radau
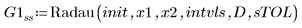
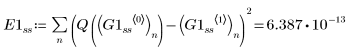
GDGL-Hybridgleichungslöser verwenden
Verwenden Sie den hybriden GDG-Löser AdamsBDF, der feststellt, ob ein System steif oder nicht-steif ist, und dementsprechend die Funktion Adams oder BDF aufruft, um die Näherungslösungen zu finden, und vergleichen Sie die Ergebnisse mit der genauen Lösung von Q.
1. AdamsBDF
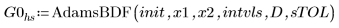
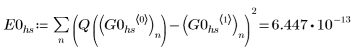
Konklusion
• Innerhalb der GDG-Löser für nicht-steife Systeme geben die Funktionen Adams und rkfixed die Lösungen mit dem kleinsten bzw. größten Fehler zurück.
• Innerhalb der GDG-Löser für steife Systeme geben die Funktionen Radau und BDF die Lösungen mit dem kleineren bzw. größeren Fehler zurück.
• Die Hybridfunktion AdamsBDF gibt einen Wert zurück, der kleiner ist als beide Werte, die von Adams oder BDF zurückgegeben werden.
• Allgemein geben die Funktionen Radau und rkfixed die Lösungen mit dem kleinsten bzw. größten Fehler zurück.
Ergebnisse vergleichen
1. Plotten Sie die von den GDG-Lösern für nicht-steife Systeme zurückgegebenen Lösungen mit dem kleinsten (Adams, G0nss) und größten (rkfixed, G1nss) Fehler:
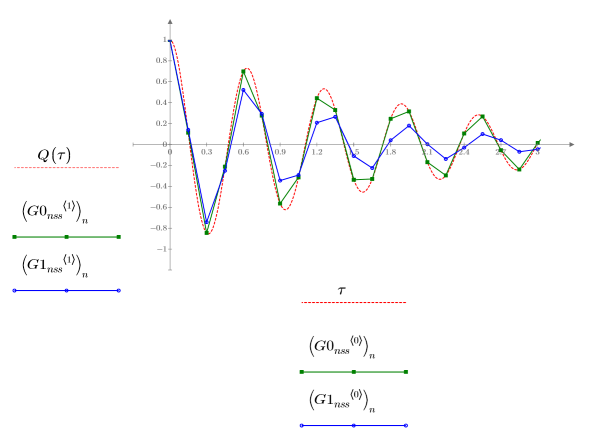
Die beiden zurückgegebenen Lösungen unterscheiden sich deutlich von Q.
2. Plotten Sie die von den GDG-Lösern für steife Systeme zurückgegebenen Lösungen mit dem kleinsten (Radau, G1ss) und größten (BDF, G0ss) Fehler:
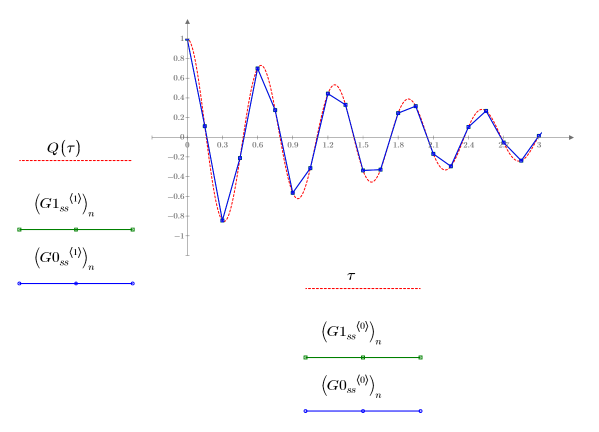
Die beiden Lösungen sind anscheinend in Bezug auf Q identisch.
3. Plotten Sie die Lösungen mit dem kleinsten (Radau, G1ss) und dem größten (rkfixed, G1nss) Fehler, die von den GDG-Lösern für steife und nicht-steife System zurückgegeben wurden:
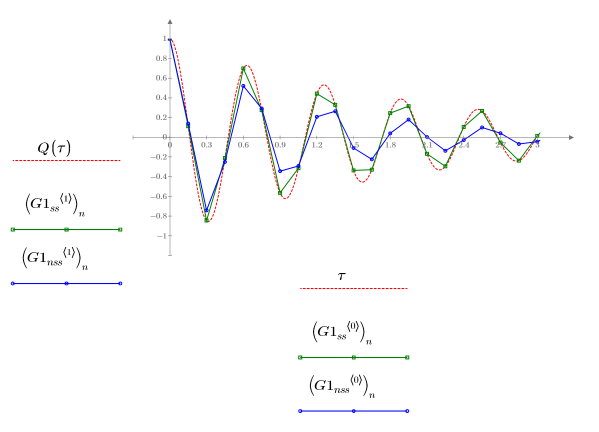
Die Funktion Radau, ein Gleichungslöser für steife Systeme, gibt die beste Näherung an die Lösung von Q zurück.