Beispiel: Konvexe Hülle

Funktionen > Bildverarbeitung > Extraktion von Elementen > Beispiel: Konvexe Hülle

Beispiel: Konvexe Hülle

Verwenden Sie die Funktion cnvxhull, um die konvexe Hülle der Pixel mit dem Intensitätswert fg für den Vordergrund in Matrix M zu suchen. Die Ausgabe ist binarisiert und weist den Wert 1 innerhalb der konvexen Hülle und den Wert 0 außerhalb auf. Der verwendete Algorithmus wird in Digital Picture Processing von A. Rosenfeld und A. C. Kak, Seite 269, 1982 beschrieben.

Für die Suche nach der Hülle werden P1 als linkster und höchster Punkt der Pixel in M und L1 als die horizontale Linie durch P1 angegeben. Danach wird L1 um P1 gedreht, bis die Linie auf den Wert fg in der Gruppe von Pixeln trifft. Mit dem Aufruf der resultierenden gedrehten Linie L2 und mit P2 als dem von P1 am weitesten entfernten Punkt auf L2 wird der Algorithmus anschließend wiederholt, bis Pn = P1. Die Vereinigungsmenge von {P1, P2, ... , Pn-1} sind die Eckpunkte der konvexen Hülle.

Weitere Informationen zur Verwendung dieses Beispiels finden Sie unter Bildverarbeitungsbeispiele.

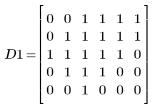
1. Definieren Sie eine Eingabematrix.

Zum Kopieren dieses Ausdrucks klicken

<region id="ID0EM34Z" top="264" left="24" width="118.693333333333" height="86.969" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math>
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id label="None">D</id>
      <matrix rows="5" cols="6">
        <real>0</real>
        <real>0</real>
        <real>2</real>
        <real>0</real>
        <real>0</real>
        <real>0</real>
        <real>0</real>
        <real>1</real>
        <real>0</real>
        <real>0</real>
        <real>1</real>
        <real>0</real>
        <real>2</real>
        <real>0</real>
        <real>2</real>
        <real>0</real>
        <real>1</real>
        <real>0</real>
        <real>1</real>
        <real>1</real>
        <real>1</real>
        <real>0</real>
        <real>1</real>
        <real>0</real>
        <real>0</real>
        <real>2</real>
        <real>0</real>
        <real>1</real>
        <real>0</real>
        <real>0</real>
      </matrix>
    </define>
    <resultFormat>
      <decimal precision="round-trip-decimal-places" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
      <matrix size="12,12" offset="0,0" />
    </resultFormat>
  </math>
</region>

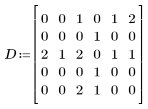
2. Berechnen Sie die konvexe Hülle der Gruppe mit dem Pixelwert 1 für den Vordergrund.

Zum Kopieren dieses Ausdrucks klicken

<region id="ID0EK54Z" top="432" left="24" width="129.718333333333" height="86.969" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math>
    <eval xmlns="http://schemas.mathsoft.com/math50">
      <id>D1</id>
      <result>
        <matrix rows="5" cols="6">
          <real>0</real>
          <real>0</real>
          <real>0</real>
          <real>0</real>
          <real>0</real>
          <real>0</real>
          <real>1</real>
          <real>1</real>
          <real>0</real>
          <real>0</real>
          <real>1</real>
          <real>1</real>
          <real>1</real>
          <real>1</real>
          <real>0</real>
          <real>1</real>
          <real>1</real>
          <real>1</real>
          <real>1</real>
          <real>1</real>
          <real>1</real>
          <real>1</real>
          <real>1</real>
          <real>1</real>
          <real>0</real>
          <real>0</real>
          <real>1</real>
          <real>1</real>
          <real>0</real>
          <real>0</real>
        </matrix>
      </result>
    </eval>
    <resultFormat>
      <decimal precision="round-trip-decimal-places" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
      <matrix size="12,12" offset="0,0" />
    </resultFormat>
  </math>
</region>

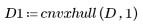
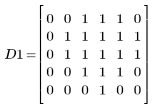
Die konvexe Hülle enthält alle Pixel mit dem Wert 1 der ursprünglichen Matrix. Es handelt sich dabei um die kleinste konvexe Gruppe.

3. Wählen Sie für die Vordergrundpixel den Wert 2 aus, und berechnen Sie die konvexe Hülle neu.

Zum Kopieren dieses Ausdrucks klicken

<region id="ID0EMA5Z" top="648" left="24" width="129.718333333333" height="86.969" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math>
    <eval xmlns="http://schemas.mathsoft.com/math50">
      <id>D1</id>
      <result>
        <matrix rows="5" cols="6">
          <real>0</real>
          <real>0</real>
          <real>1</real>
          <real>0</real>
          <real>0</real>
          <real>0</real>
          <real>1</real>
          <real>1</real>
          <real>1</real>
          <real>0</real>
          <real>1</real>
          <real>1</real>
          <real>1</real>
          <real>1</real>
          <real>1</real>
          <real>1</real>
          <real>1</real>
          <real>1</real>
          <real>1</real>
          <real>0</real>
          <real>1</real>
          <real>1</real>
          <real>1</real>
          <real>0</real>
          <real>0</real>
          <real>1</real>
          <real>1</real>
          <real>0</real>
          <real>0</real>
          <real>0</real>
        </matrix>
      </result>
    </eval>
    <resultFormat>
      <decimal precision="round-trip-decimal-places" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
      <matrix size="12,12" offset="0,0" />
    </resultFormat>
  </math>
</region>

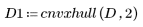
4. Überlagern Sie ein binäres Bild eines Maiskorns mit dessen konvexer Hülle, um die Nützlichkeit der Hülle für die Beschreibung der Kontur und der Löcher in einem Bild zu demonstrieren.

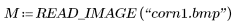
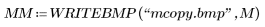
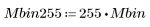
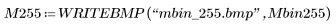
5. Suchen Sie die konvexe Hülle der weißen Pixel (1) in dem binarisierten Bild, und subtrahieren Sie anschließend das Bild von der Hülle, um das konvexe Defizit zu ermitteln. Anstatt die Subtraktion direkt auszuführen, werden das binarisierte Bild und die konvexe Hülle skaliert, sodass der Abschnitt außerhalb der Hülle in grau, die Bildpixel in schwarz und das konvexe Defizit in weiß dargestellt werden.

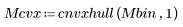
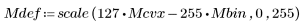
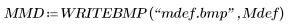
6. Zeigen Sie die Bilder M, Mbin255 und Mdef nebeneinander an.

(corn1.bmp)

(mbin_255.bmp)

(mdef.bmp)

Die Außenseite der Hülle ist in M in grau, das Bild Mbin55 in schwarz und die Abweichung von der Konvexität im abschließenden Bild Mdef in weiß dargestellt.

Zugehörige Themen

Konvexe Hülle

War dies hilfreich?