Beispiel: Komplexe Zahlen, polare Schreibweise
Verwenden Sie die Funktionen für komplexe Zahlen, um eine komplexe Zahl zu konstruieren, ihre polare Form anzuzeigen und ihre konjugiert-komplexe Zahl zu finden.
1. Geben Sie eine komplexe Zahl ein:
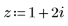
Geben Sie für die imaginäre Einheit eine Konstante ein, auf die unmittelbar i oder j folgt, beispielsweise "1i" oder "1j". Wenn Sie auf den obigen komplexen Zahlenausdruck klicken, können Sie feststellen, dass "2i" tatsächlich 2i ist und nicht 2 * i, dass es also als imaginäre Einheit definiert ist und nicht als 2 Mal die Variable i.
2. Zeigen Sie die polare Form von z an:
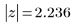
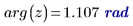
3. Rekonstruieren Sie die ursprüngliche rechteckige Form:
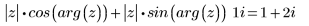
4. Ermitteln Sie die konjugiert-komplexe Zahl von z, indem Sie deren imaginäre Komponente von deren reeller Komponente subtrahieren:
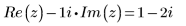
5. Ermitteln Sie mithilfe des Konjugiert-Komplex-Operators die konjugiert-komplexe Zahl von z: