Beispiel: Cepstrum und komplexes Cepstrum
Verwenden Sie die Funktionen cepstrum und ccepstrum, um das Cepstrum und das komplexe Cepstrum eines reellwertigen Mehrkanalsignals zu berechnen.
Das Cepstrum ordnet Faltung und Entfaltung zu Addition und Subtraktion im Frequenzbereich zu und findet Anwendung in der Verarbeitung von Sprach- und geophysikalischen Signalen.
cepstrum
Das Cepstrum der Sequenz x(n) wird durch die folgende Formel angegeben:
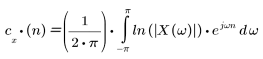
wobei X(ω) der Fourier-Transformation von Sequenz x(n) entspricht.
Dies ist die Definition der inversen Transformation nach Anwendung eines natürlichen Logarithmus auf die Fourier-Transformation von x(n). Der Logarithmus ordnet Faltung im Zeitbereich zu Addition im Frequenzbereich zu, wodurch das Cepstrum zu einem bequemen Werkzeug für die Signalentfaltung wird, die der Subtraktion zugeordnet ist.
1. Definieren Sie den Bereich von n.
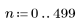
2. Definieren Sie die Sequenzfunktion x.
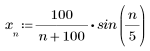
3. Plotten Sie die Sequenzfunktion x.
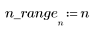
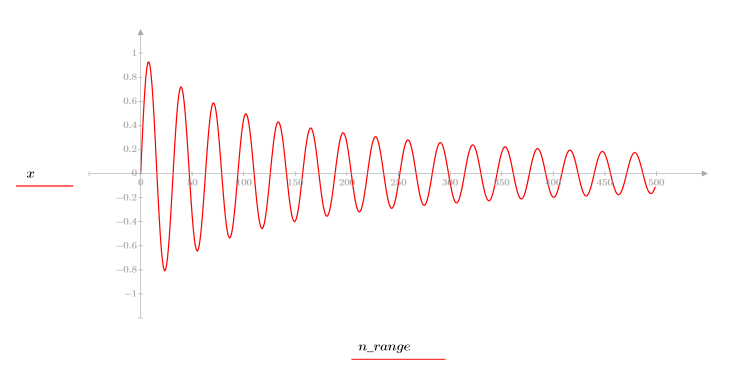
4. Berechnen Sie das Cepstrum, und plotten Sie die resultierende Funktion.
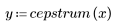
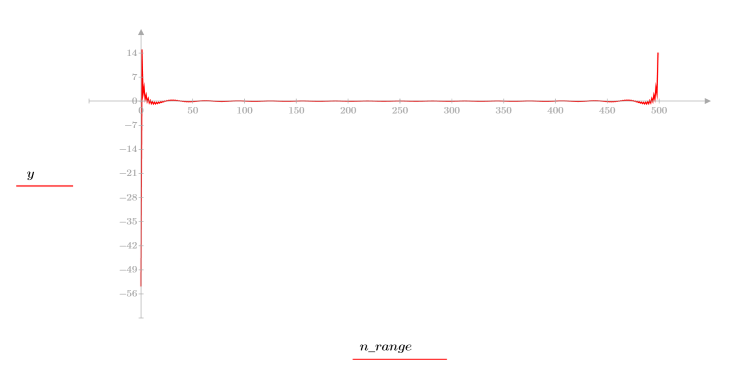
5. Verwenden Sie die Funktion recenter, um das Ergebnis erneut zu zentrieren, um das erste Element in die Mitte zu bringen.
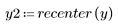
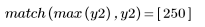
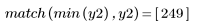
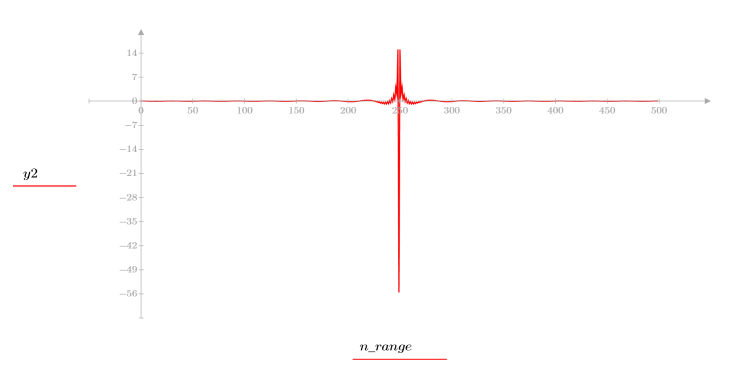
Das ursprüngliche Signal kann nicht mit dem Cepstrum wiederhergestellt werden, da die Phaseninformationen nicht beibehalten werden.
ccepstrum
Die komplexe cepstrum-Funktion wird durch den folgenden komplexen Logarithmus angegeben.
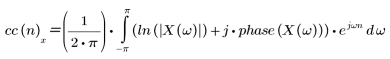
Dabei entspricht X(ω) der Fourier-Transformation der Sequenz x(n), während die Phase zur Erfassung der Phaseninformationen der jeweiligen Sequenz verwendet wird.
Der Vergleich der Ccepstrum-Daten des Ausgabesignals mit denen der Eingabe- und Kanalsequenzen zeigt, dass die Ccepstrum-Daten der Ausgabe der Summe der Ccepstrum-Daten von Eingabe und Kanal entsprechen. Dies entspricht weitestgehend dem Hinzufügen der Spektren von zwei Signalen zum Frequenzbereich, was jedoch im Zeitbereich ausgeführt wird.
Im folgenden Beispiel wird ein Signal durch einen Kommunikationskanal simuliert, in dem Echos eingeführt werden (nach Abschnitt 12.8.1. von Oppenheim und Schäfer, Prentice-Hall, 1989).
1. Definieren und plotten Sie die Kanalantwort als nichtrekursiven Filter, der abgeschwächte Kopien einer anderen Sequenz (Echos) einführt.
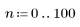
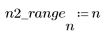
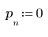
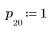
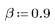
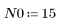
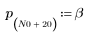
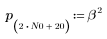
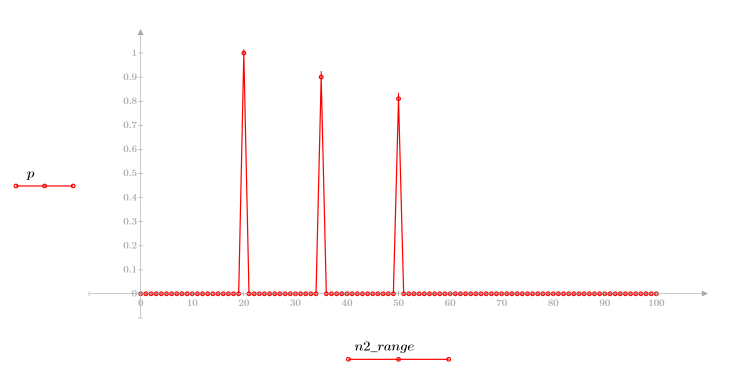
2. Definieren und plotten Sie die Sequenz v, die mit der Kanalantwort gefaltet wird.
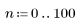
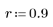
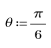
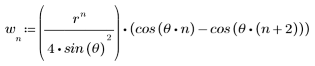
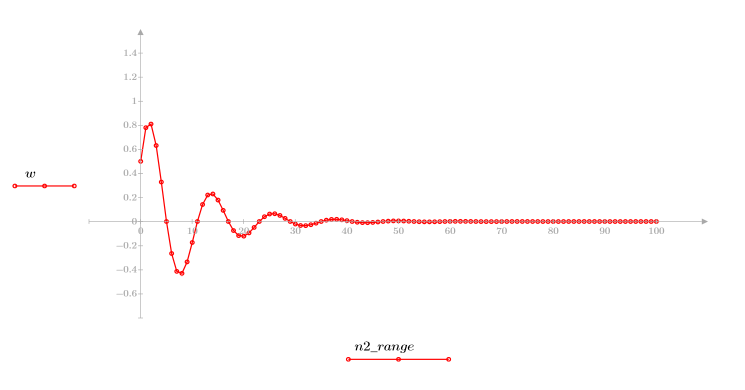
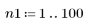
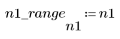
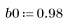
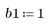
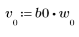
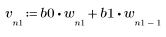
3. Verwenden Sie die Funktion response, um die n-fache Vektorantwort von Eingangsvektor p für einen nichtrekursiven Filter mit dem Koeffizienten-Array v (die Kommunikationskanalfunktion v) abzurufen.
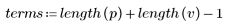
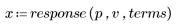
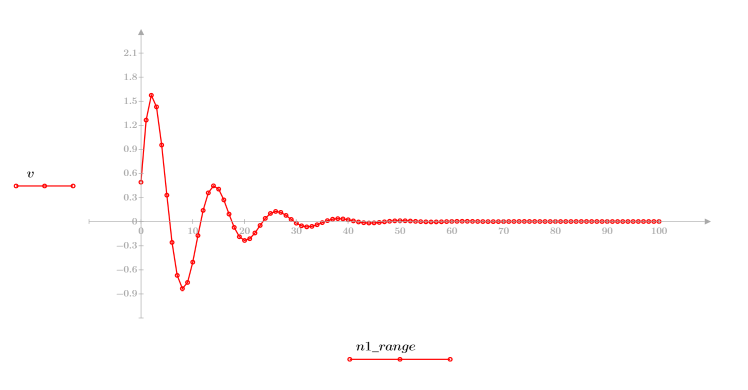
4. Plotten Sie die Antwortfunktion.
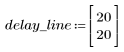
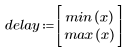
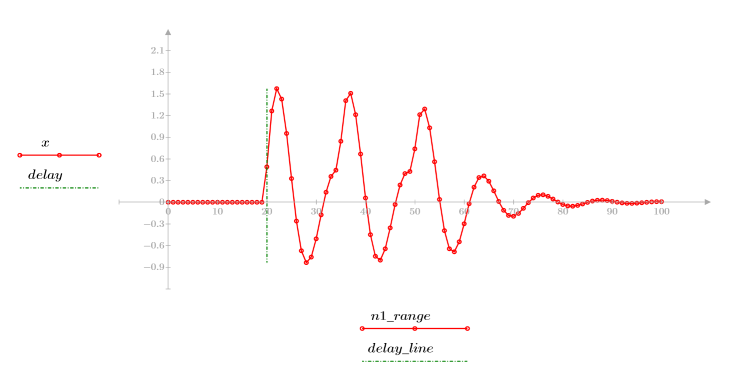
◦ Die resultierende Sequenz entspricht der Faltung der Eingabefunktion p und der Kommunikationskanalfunktion v.
◦ Die Sequenz zeigt das ursprüngliche Signal und die verzögerten Replikate an.
5. Vergleichen Sie die Ccepstrum-Daten des Ausgabesignals mit den Cepstra-Daten der ursprünglichen Sequenzen. Zentrieren Sie die Ergebnisse neu, um den Vergleich zu vereinfachen.
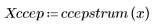
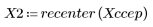
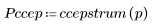
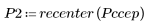
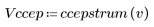
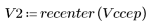
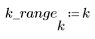
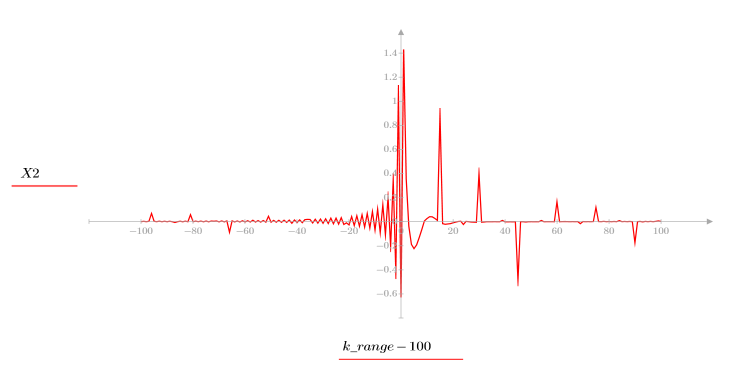
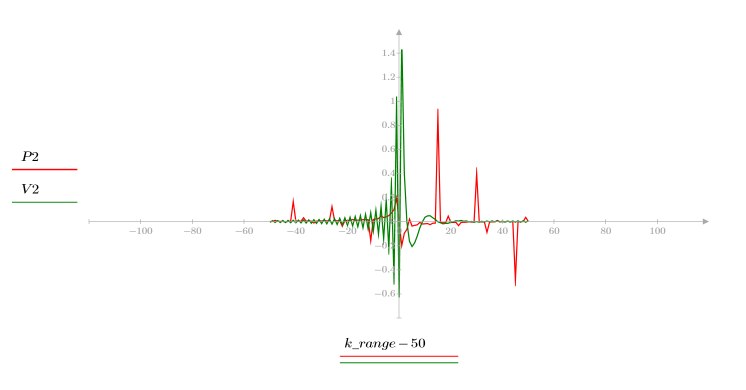
Die Diagramme oben zeigen, dass die Ccepstrum-Daten des Ausgabesignals der Summe der komplexen Cepstra-Daten der beiden Sequenzen entsprechen, die miteinander gefaltet wurden.