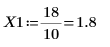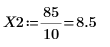Beispiel: Bessel-Funktionen erster Art
Zeigen Sie die Beziehung zwischen den Funktionen J0, J1 und Jn an. Zeigen Sie auch die Beziehungen zwischen diesen Funktionen und ihren skalierten Versionen an.
1. Legen Sie zwei Schrittbereichsvariablen fest:
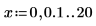
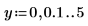
2. Plotten Sie die Funktionen J0 und J1. Fügen Sie dem Diagramm die Funktion Jn zweiter Ordnung hinzu:
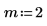
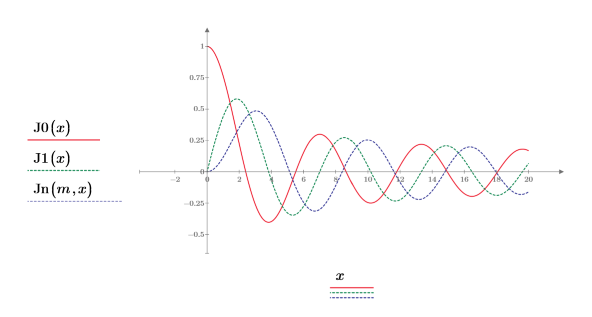
3. Erstellen Sie ein Diagramm, um zu zeigen, dass J0(y)=Jn(0,y) Setzen Sie die Teilstrichwerte zurück, um die x-Achse zu vergrößern, damit mehr Details angezeigt werden:
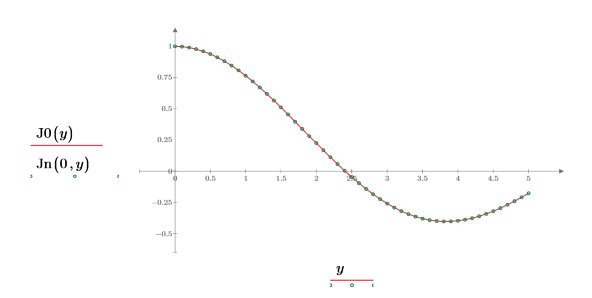
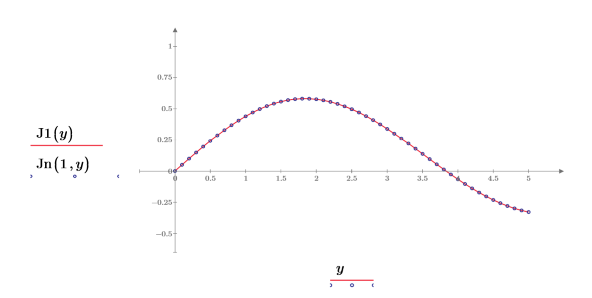
4. Erstellen Sie ein Diagramm, um zu zeigen, dass J1(y)=Jn(1,y) Setzen Sie die Teilstrichwerte zurück, um die x-Achse zu vergrößern, damit mehr Details angezeigt werden:
5. Verwenden Sie die symbolische Auswertung, um die Beziehung zwischen jeder Bessel-Funktion erster Art und ihrer skalierten Version anzuzeigen:
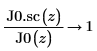
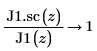
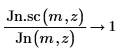
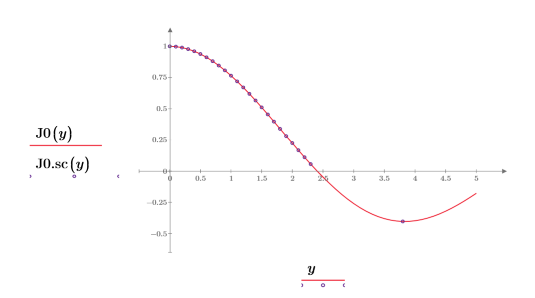
6. Erstellen Sie ein Diagramm, um Folgendes zu zeigen:
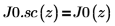
J0.sc enthält komplexe Elemente; wenden Sie daher zuerst die Funktion Re an, um nur den Realteil der Zahlen anzuzeigen.
7. Berechnen Sie die Koordinaten der ersten beiden Spitzenwerte von J1. Verwenden Sie die Funktionen augment und localmax, um die Spitzenwerte zu identifizieren, die innerhalb des angegebenen Bereichs liegen:
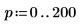
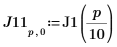
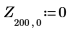
Die Funktion localmax erfordert eine Eingabematrix mit zwei Spalten. Die Funktion augment wird verwendet, um eine solche Matrix zu erstellen.
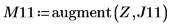
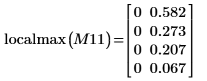
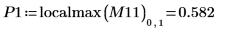
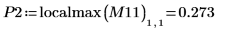
8. Verwenden Sie die Funktion match, um die horizontalen Koordinaten der Spitzenwerte zu suchen. Reduzieren Sie den Wert von TOL, um möglichst genaue Ergebnisse zu erhalten:
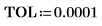
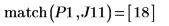
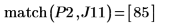
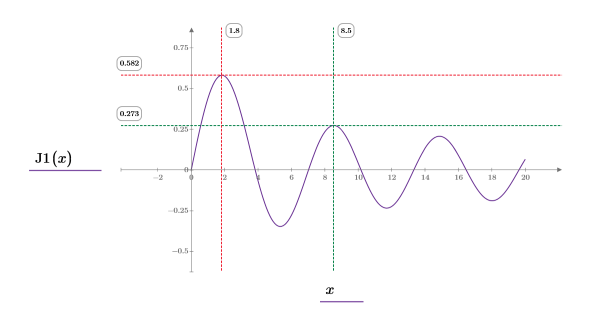
9. Fügen Sie dem Diagramm Markierungen hinzu, um die beiden ersten Spitzenwerte zu markieren:
Die Schrittbereichsvariable hat einen Schrittwert von 0.1. Das bedeutet, dass die Spitzenwerte bei 1/10 des Elementindex auftreten, der von der Funktion match oder 1.8 bzw. 8.5 identifiziert wird.