Beispiel: Bessel-Funktionen
Verwenden Sie die sphärischen Bessel- und die sphärischen Hankel-Funktionen, um die Lösungen für die Schrödinger-Gleichung im 3D-Gevierttopf (einem Atom) zu finden.
Die Lösung stellt die zulässigen Energien dar, bei denen die inneren und äußeren Wellenfunktionen gleiche Werte und erste Ableitungen haben. Diese Energien existieren für jeden Wert des Drehimpulses (L).
1. Definieren Sie die Masse, das Plancksche Wirkungsquantum und den Radius des Kerns:
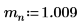
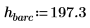
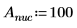
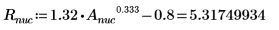
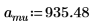
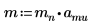
2. Legen Sie den Drehimpuls auf null fest:
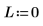
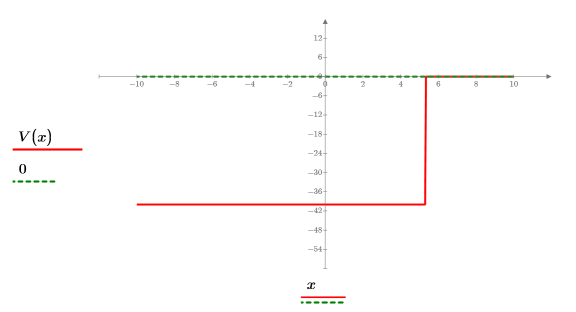
3. Definieren und plotten Sie die potenzielle Energie des Topfes:
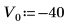
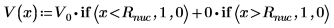
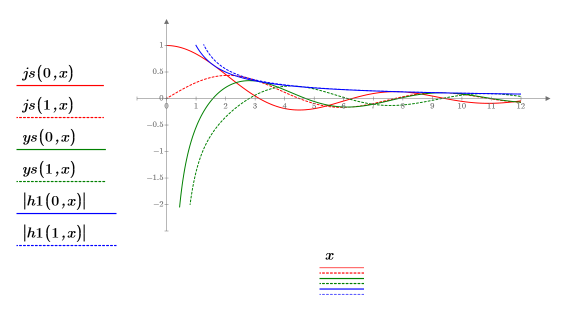
4. Verwenden Sie die sphärischen Bessel-Funktionen und die sphärischen Hankel-Funktionen, um die Lösungen zu finden:
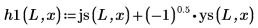
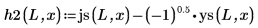
5. Definieren Sie für die gebundenen Status E < 0 die Wellenfunktionen für die erste Energiestatuslösung innerhalb und außerhalb des Topfes:
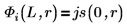
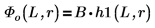
B ist die relative Normalisierung.
6. Definieren Sie die Ausbreitungskonstanten:
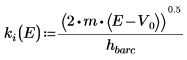
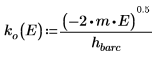
Das Argument für die Lösung außerhalb des Topfes ist imaginär, da die Welle außerhalb des Potenzialtopfes abklingt.
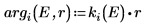
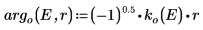
7. Passen Sie die Wellenfunktionen am Rand des Topfes (dem Radius des Kerns) an, um die relative Normalisierung zu bestimmen:
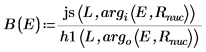
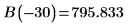
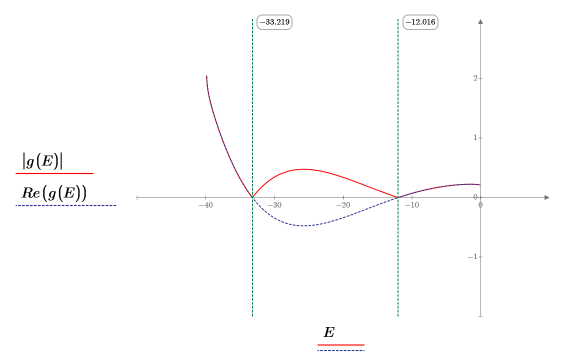
8. Passen Sie die Ableitungen an. Bestimmen Sie die Eigenwerte, indem Sie den Punkt ermitteln, an dem die Ableitungen gleich sind.
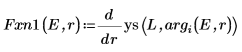
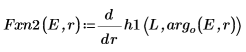
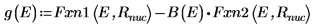
9. Stellen Sie zwei Schätzwerte für E bereit:
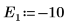
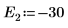
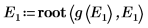
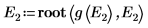
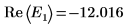
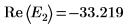
10. Plotten Sie g(E) im Vergleich zu E, und fügen Sie vertikale Markierungen hinzu, um die zwei Stammpunkte anzuzeigen: