Ableiten von Startbedingungen für ein Differentialgleichungssystem erster Ordnung
Die folgenden Funktionen werden bei Randwertproblemen verwendet, bei denen nicht alle Anfangsbedingungen bekannt sind.
• bvalfit(v1, v2, x1, x2, xf, D, load1, load2, scoreb)
• sbval(v1, x1, x2, D, load1, scorei)
Gibt einen Vektor mit den Anfangswerten zurück, die bei x1 für die Differentialgleichung erster Ordnung oder das Differentialgleichungssystem erster Ordnung, das in D benannt ist, nicht festgelegt wurden. Diese Anfangswerte können anschließend in einem der Lösungsverfahren für Differentialgleichungssysteme erster Ordnung verwendet werden. Wenn Sie einige Werte der Lösung und die ersten n − 1 Ableitungen bei einem Zwischenwert kennen, verwenden Sie bvalfit. Diese Funktion ist vor allem dann hilfreich, wenn die Ableitung eine Unstetigkeit innerhalb des Integrationsintervalls aufweist. Wenn Sie einige Werte an den Anfangs- und Endpunkten kennen, verwenden Sie sbval. Das Grenzwertproblem wird in ein Anfangswertproblem umgewandelt, indem man von den Endpunkten ausgeht und die Trajektorien der Lösung sowie ihrer Ableitungen an einem Zwischenpunkt zusammengepasst werden.
Argumente
• v1, v2 sind Vektoren aus reellen Schätzwerten für die Anfangswerte, die bei x1 nicht festgelegt wurden.
• x1, x2 sind die reellen Endpunkte des Intervalls, in dem die Lösung für Differentialgleichungen ermittelt wird.
• xf ist ein reeller Zwischenpunkt zwischen x1 und x2, an dem die Trajektorien der Lösungen gleich sein müssen.
• D(x, y) ist eine n-elementige, vektorwertige Funktion der unabhängigen Variablen x und ein Vektor mit Funktionen y, der die Gleichungen für die ersten Ableitungen aller unbekannten Funktionen im System von gewöhnlichen Differentialgleichungen enthält.
Zum Erstellen dieses Vektors müssen Sie Ihre Gleichungen linksseitig mit einer ersten Ableitung der jeweiligen Gleichung – ohne Multiplikatoren und Ableitungen höherer Ordnung in der Gleichung – konvertieren. Z.B. muss eine einzelne gewöhnliche Differentialgleichung der Funktion y(x), die eine zweite Ableitung enthält, als System von Gleichungen in y0(x) und y1(x) geschrieben werden, wobei die erste Ableitung von y0 y1 ist. Die folgende gewöhnliche Differentialgleichung mit einer einzelnen Funktion wird mithilfe der Vektor-Indizes für den Löser umgeschrieben:
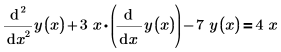
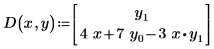 | mit der implizierten linken Seite | 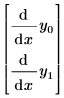 |
• load1(x1, v1), load2(x2, v2) sind reelle, vektorwertige Funktionen, deren Elemente den Werten von yn in x1 und x2 entsprechen. Einige dieser Werte sind bekannte Anfangsbedingungen. Unbekannte Werte werden auf entsprechende Schätzwerte aus v1 und v2 gesetzt.
• scoreb(xf, y) ist eine reelle, vektorwertige Funktion, mit der festgelegt wird, auf welche Art und Weise die Lösungen bei xf übereinstimmen sollen. Gewöhnlich müssen Sie scoreb(xf, y):= y definieren, sodass die Lösungen für alle unbekannten Funktionen bei xf übereinstimmen.
• scorei(x2, y) ist eine reelle, vektorwertige Funktion mit derselben Anzahl von Elementen wie v. Jedes Element stellt die Differenz zwischen einer Anfangsbedingung bei x2, wie ursprünglich festgelegt, und dem entsprechenden Schätzwert des Lösers dar. Der Vektor score gibt an, wie eng eine vorgeschlagene Lösung mit den Anfangsbedingungen bei x2 übereinstimmt. Ein Wert von 0 für ein beliebiges Element zeigt eine perfekte Übereinstimmung an.