範例:方程式的符號解
以符號方式求解具有一或多個未知數的方程式。
求解單一方程式
1. 鍵入下列方程式:
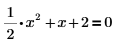
2. 插入符號計算運算子,然後在佔位符號中鍵入關鍵字 solve,再按 Enter 鍵。
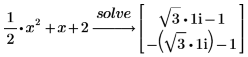
由於方程式右側為 0,因此您不需要鍵入運算式的 =0 部份。 |
3. 以小數格式鍵入常數 2 為 2.0,傳回浮點格式的解。
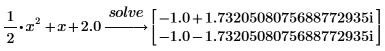
4. 求解具有一個變數的方程式。
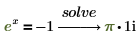
5. 求解具有多項變數的方程式。
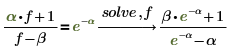
當方程式含有多項變數時,您必須指定要求解的變數。 |
6. 求解四階多項式。

上述結果顯示四階多項式的符號解會得出四個數值解。 |
7. 求解具有參數化係數的多項式根式解。
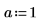
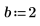
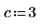
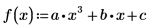
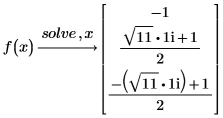
求解方程式與等式系統
您可以將數個方程式與等式組合在向量中,作為一個聯立方程式來解出。
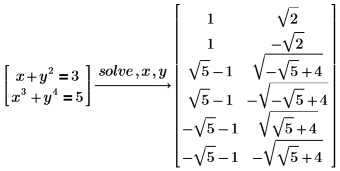
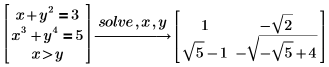
求多項式的根
根據預設,PTC Mathcad 最多可求 4 次多項式方程式的根式解。此根式解使用一般算數運算求解。
1. 求解下列多項式:
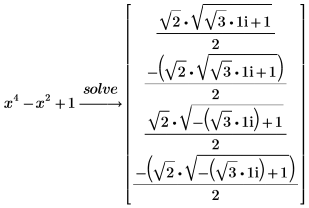
十九世紀數學家 Galois 證明 5 次及 5 次以上的多項式無法求得根式解。針對這些多項式,PTC Mathcad 會傳回根的近似數值。 |
2. 求解 5 次多項式。

上述結果顯示五階多項式的符號解會得出五個數值解。 |
假設變數域
使用關鍵字 assume 假設問題中的變數域;例如,假設其為實數。
1. 求解假設 x 為實數的方程式。
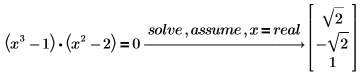
PTC Mathcad 只會傳回方程式的實數解。 |
2. 使用 RealRange 求解值域 (0, 2) 的實數解。
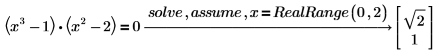
3. 鍵入 x=integer 只求解整數解。
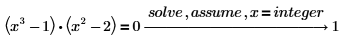
4. 使用 assume 限制符號計算中的變數域。
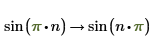
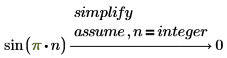
傳回方程式的詳解
在求解之後新增修飾符 fully,可傳回方程式的詳解。
1. 使用函數 clear.sym 清除 a 的上一個符號值。
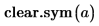
2. 使用 fully 傳回有效解的 a 值。
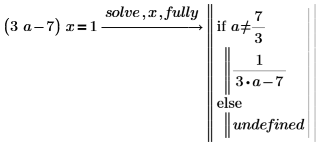
3. 使用詳細結果定義函數。
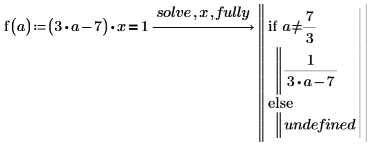
4. 計算 a=3 及 a=7/3 時的函數:
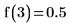
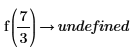
具有週期解的方程式
針對具有週期解的方程式,PTC Mathcad 會傳回單一解,後面接著將週期的整數倍數加上第一個解的運算式。
1. 使用 fully 計算 sin(x)。
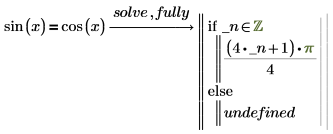
If 語句後的運算式表示 pi/4 加上 pi 的所有整數倍數。PTC Mathcad 會插入代表任意整數之新產生的變數 _n。在產生的變數之前插入底線,可避免與可能在工作表中其他位置定義的其他變數,發生名稱衝突。 |
2. 新增修飾符 using,後面接著使用布林等於運算子所撰寫的方程式,以將產生的變數設為等於新變數。
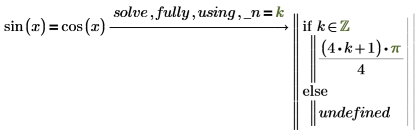
若您在 using 之後指定的變數不是 solve 傳回的產生變數,PTC Mathcad 會傳回錯誤。