範例:乘冪遞歸
使用 genfit 函數
1. 定義數據集。
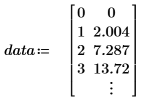
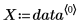
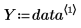
2. 定義擬合函數,其中 A 與 b 為未知數。
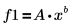
3. 定義函數向量。
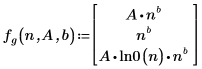
4. 定義估值向量。
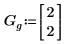
5. 使用 genfit 求解乘冪函數的係數。
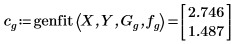
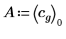
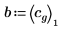
6. 使用係數 A 與 b 定義函數。
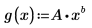
7. 繪製數據點與擬合函數。
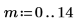
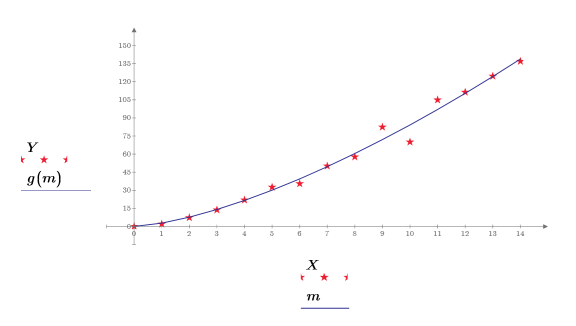
使用 pwrfit 函數
1. 定義擬合函數,其中 a、b 及 c 為未知數。
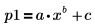
2. 定義估值向量。
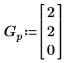
3. 使用 pwrfit 求解乘冪函數的係數。
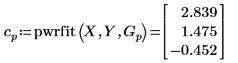
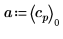
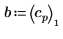
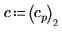
4. 使用係數 a、b 及 c. 定義函數
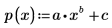
5. 繪製數據點與擬合函數。
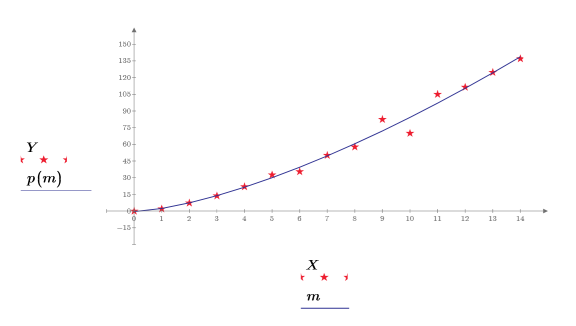
檢查擬合度
1. 使用殘差繪圖檢查模型與數據的擬合程度。
◦ 最大殘差值為:
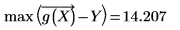
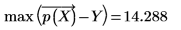
◦ 最小殘差值為:
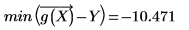
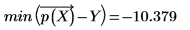
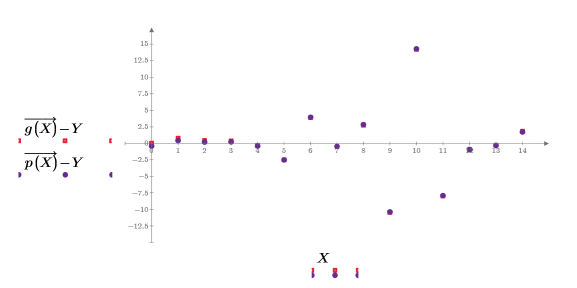
2. 使用 corr 函數計算相關係數。
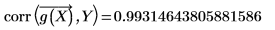
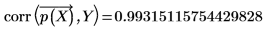
擬合度似乎比殘差繪圖顯示的程度更高。
針對存在的大型數據,特別是隨著 X 的值愈來愈大而迅速變化的乘冪或指數數據,殘差繪圖不一定是判斷擬合度的最佳工具。
加權的 genfit
根據其他參數,使用局部函數修改您傳遞至 genfit 的函數向量。
1. 定義函數以根據數據的標準差加權數據。
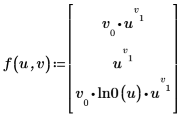
使用參數的向量輸入格式,可讓其他含有任意數目參數的擬合函數類型,輕鬆地使用加權函數。
2. 編寫程式以根據數據的標準差傳回其 genfit。

3. 定義標準差向量。

4. 傾斜原始集合的其中一個數據點。
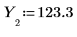
5. 呼叫程式,然後將標準差與估值的向量傳遞給程式。
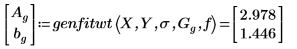
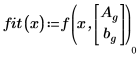
6. 呼叫不使用權重的 genfit 函數:
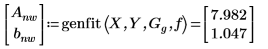
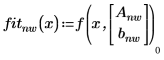
7. 繪製數據與兩個擬合函數,並進行比較。
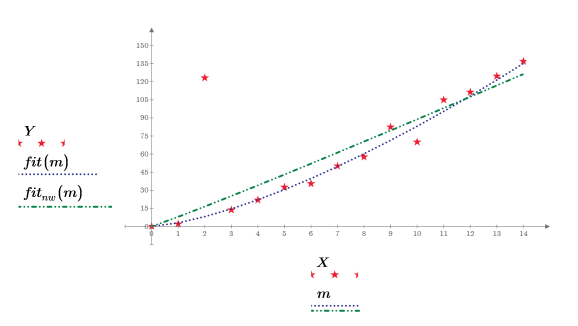
以標準差為基礎的函數可提供更佳的擬合度。