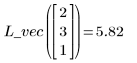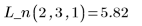範例:分段二次擬合
單變量多項式遞歸
使用區域遞歸,利用 loess 函數擬合一系列的二次函數與數據。
1. 定義下列矩陣:

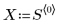
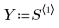
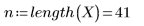
2. 定義合併區 - 各數據點附近加權窗中的總點數百分比,此係用於 loess 函數執行的連續二次擬合。
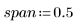
一般規則是 (span*n) 應該要 > 1,因為點數要大於 1,才能平均分配到每一個最小平方加權擬合中:
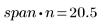
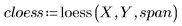
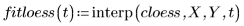
4. 呼叫 polyfit 函數將 2 階多項式擬合至數據集。
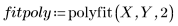
5. 繪製前文定義的兩條曲線。
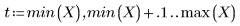
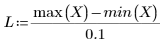
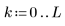
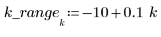
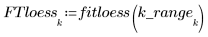
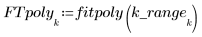
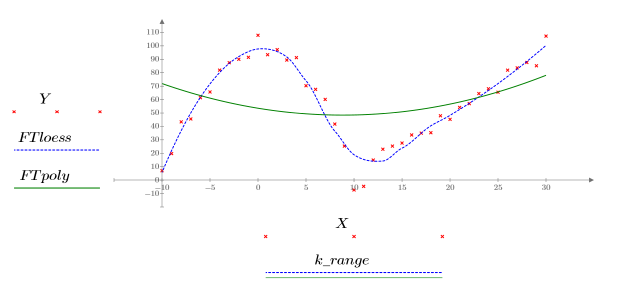
• 當合併區很大 (例如 2 或 3) 時,數據會視為具有幾近相等權重的單一二次擬合。擬合趨近於二次多項式的 polyfit 解。
• 選擇合併區沒有真正精準的規則。當合併區變大時,loess 擬合的繪圖會變得更平滑,因為擬合中會連接較少的片段。但擬合無法適切遵循數據的特性。相反地,當合併區變小時,您會發現 loess 並未收斂。
• loess 演算法的設計不適用於外推。若嘗試以原始 x 範圍以外的值計算 interp,會傳回錯誤。
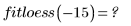
• 當數據稍有不連續的特徵,但又不想手動分段擬合,或使用複雜、不合乎自然或非線性擬合的方法時,可以使用 loess。
多變量多項式遞歸
使用 loess 函數執行多變量多項式遞歸。loess 函數最多只能擬合 4 個自變數。
1. 定義數據集。
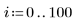
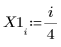
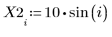
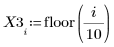
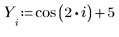
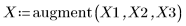
2. 定義平滑參數。
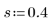
此參數的意義與單係數情況時相同。
3. 呼叫 loess 函數。
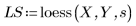
4. 呼叫 interp 內插多變量擬合函數。擬合函數可採用 n 元素的向量或一組 n 引數,此處的 n 是自變係數的數目。
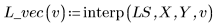
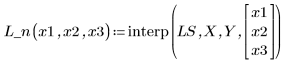
5. 使用擬合函數預測點 (2, 3, 1) 的 Y 值。