範例:非線性遞歸 2
使用 LeastSquaresFit 函數執行非線性遞歸。LeastSquaresFit 求解器為求解非線性遞歸問題提供最大的彈性。它可讓您輸入所有相依參數、參數上下限、x 值標準差,以及計算信心極限的條件約束方程式。
LeastSquaresFit
1. 定義數據集。
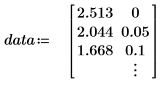
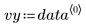
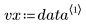
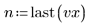
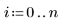
此數據擷取自 NIST 網站上所討論的範例。使用下列方程式可產生精確到 14 位的數據:
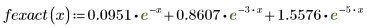
2. 定義擬合函數。
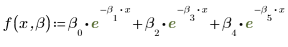
上述個別參數是向量 β 的元素。您也可以個別的變數名稱指定輸入函數,不使用向量的元素:
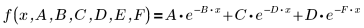
3. 提供估值。
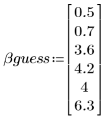
4. 定義參數的信心限制。
5. 呼叫 LeastSquaresFit 函數。
求解器使用序列二次規劃法 (SQP) 求解所得出的最小平方問題。藉由引入其他變數,原始問題會轉換成一般的等式約束非線性規劃問題,一般而言,這比其他方法更快且更穩定。
6. 檢視 LeastSquaresFit 函數傳回的輸出向量。
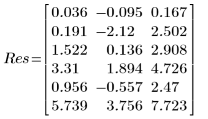
◦ 輸出的第一欄包含擬合參數的值。第二欄及第三欄分別包含參數信心區間的左邊界及右邊界。
◦ 對參數的 95% 信心限制涵蓋相當大的範圍,顯示擬合很困難,且個別參數也會有很大的差異。因此,擬合參數的值與 NIST 網站上所記錄的正確值不同:
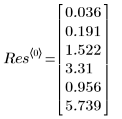

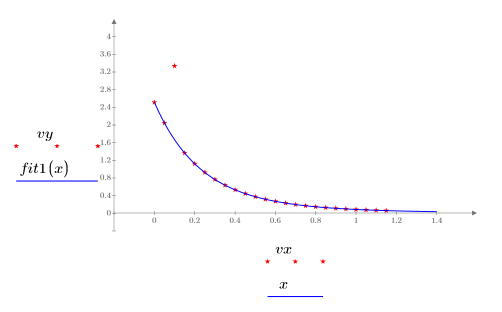
7. 繪製數據、最小平方擬合及 NIST 擬合。
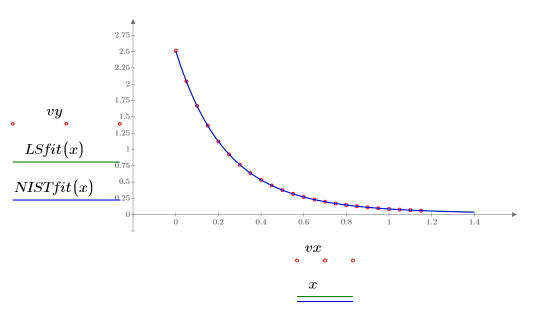
8. 比較最小平方擬合與原始數據:
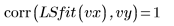
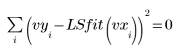
擬合趨近於收斂,但可得益於調整收歛公差。透過其中一個 LeastSquaresFit 函數的選用引數即可完成。
條件約束、標準差及公差
有數個選用引數可用於 LeastSquaresFit:
• 標準差向量
• 上下邊界矩陣
• 精確度
您可單獨使用這些選用引數,但若輸入多個引數,引數的順序會有影響。
1. 干擾其中一個數據值,以模擬誤測。
2. 指定上下邊界以約束擬合值。
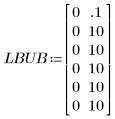
在預期參數值範圍外的界限設定良好,因為本例中沒有已知的特定界限。
3. 為每個 y 值設定標準差向量,遮罩離群值。
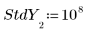
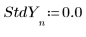
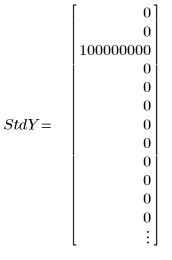
◦ 標準差中的大值 108 會有效移除計算的誤測。
◦ 將標準差向量當成引數輸入 LeastSquaresFit 函數時,求解器會最小化下列函數
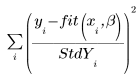
若某個點的標準差為 0,即表示該點使用原始未偏離的函數,亦即 StdYi 設為 1。
4. 設定精確度,將更嚴格的收歛公差應用至計算 (預設值為 10-7)。
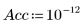
5. 呼叫 LeastSquaresFit 函數,無論有無標準差。
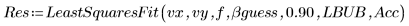
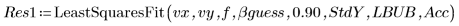
◦ 未遮罩的計算失敗,因為信心限制太大。
◦ 新參數較近似 NIST 值:
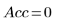
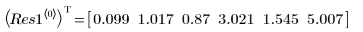
6. 以離群值及遮罩擬合來繪製數據。
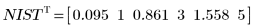
參照
此範例的數據取自 C. Lanczos 所著之 Applied Analysis (應用分析),Prentice Hall 於 1956 年出版,第 272-280 頁,如 NIST Statistical Reference Dataset Archive (NIST 統計參考文獻資料庫) 中所記錄。