範例:Kelvin 函數
1. 繪製第零階函數 ber 與 bei:
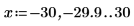
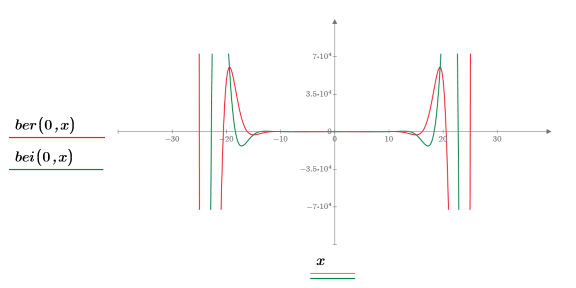
這兩個函數呈對稱。
2. 重設刻度線值放大 x 軸,以顯示隨著階數增加,ber 與 bei 函數的兩個尖峰會如何變化:
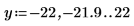
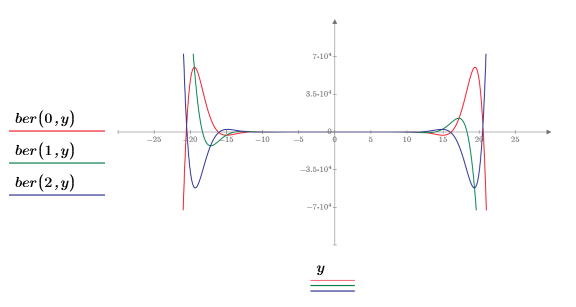
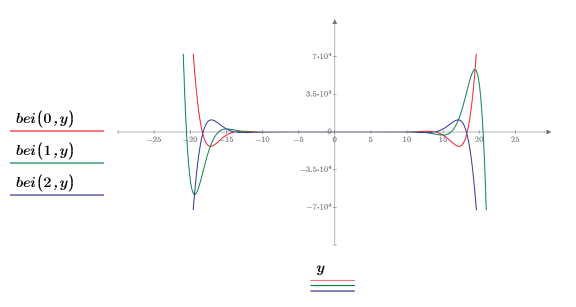
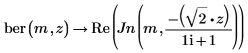
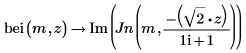
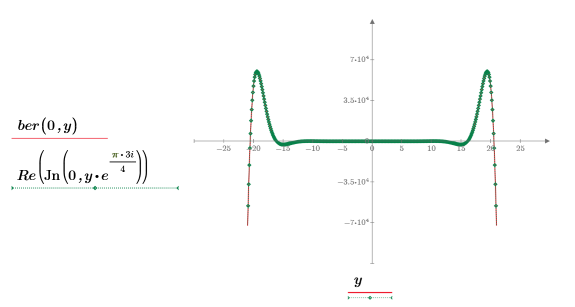
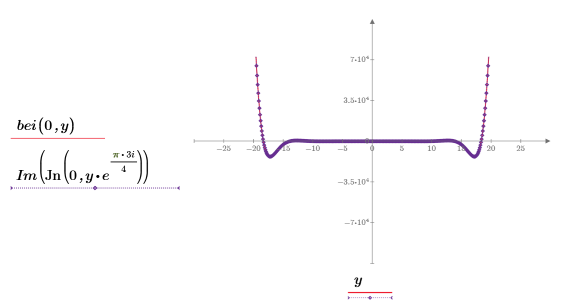
此範例著重於 ber 函數,但相同的觀測也適用於函數 bei。
4. 使用函數 ber 定義向量 Z1:
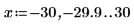
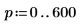
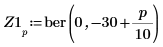
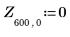
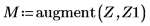
5. 求解函數 ber 的局部最小值:

當 m=0 時,ber 函數具有 8 個最小值。此函數呈對稱。高階函數具有不同的最小值數,且位置與振幅也不同。
6. 求解函數 ber 的局部最大值:

當 m=0 時,ber 函數具有 7 個尖峰。此函數呈對稱。高階函數具有不同的最大值數,且位置與振幅也不同。
7. 求解四個右側最小值的垂直座標。
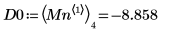
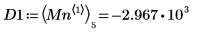
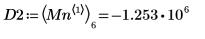
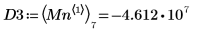
8. 使用函數 match 求解每個相符最小值的索引,然後求解對等的水平座標。
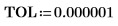
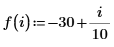
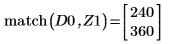
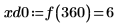
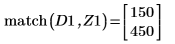
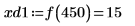
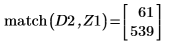
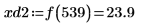
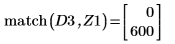
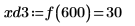
9. 求解四個右側最大值的垂直座標。
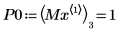
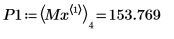
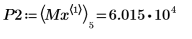
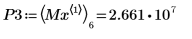
10. 使用函數 match 求解每個相符最大值的索引,然後求解對等的水平座標。
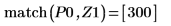
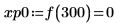
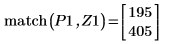
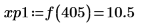
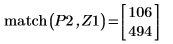
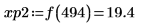
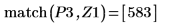
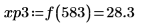
最大值與最小值振幅的值域大不相同,因此很難在同一個繪圖上檢視所有的值。 |
11. 使用標記顯示第一個最小值 (D0) 與第一個最大值 (P0):
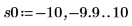
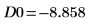
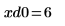
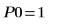
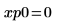
一如預期,此圖表會在 y 軸左側顯示第二個最小值。
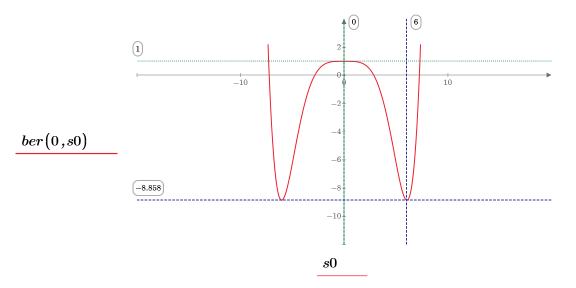
12. 使用標記顯示下一個最小值 (D1) 與下一個最大值 (P1):
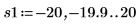
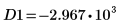
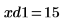
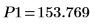
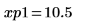
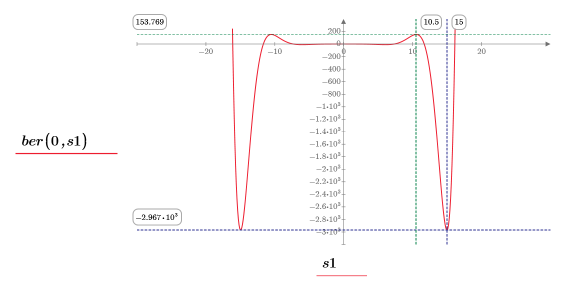
一如預期,此圖表會在 y 軸左側顯示第二個最小值與第二個最大值。
13. 使用標記顯示下一個最小值 (D2) 與下一個最大值 (P2):
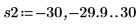
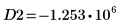
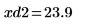
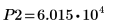
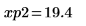
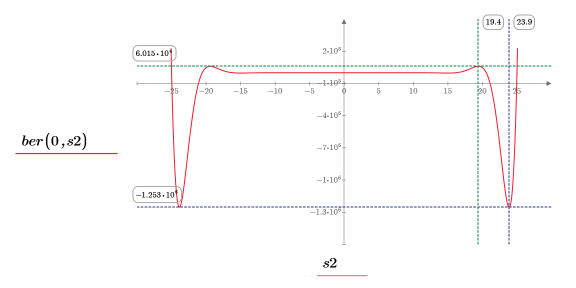
一如預期,此圖表會在 y 軸左側顯示第二個最小值與第二個最大值。
14. 使用標記顯示下一個最小值 (D3) 與下一個最大值 (P3):
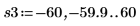
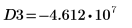
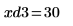
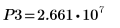
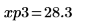
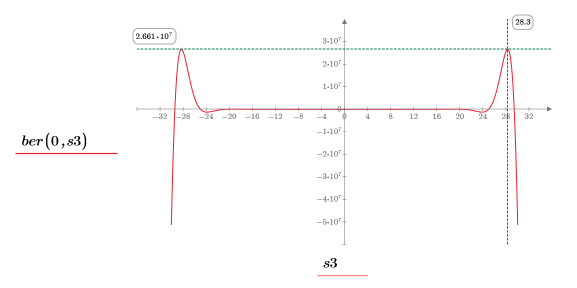
一如預期,此圖表會在 y 軸左側顯示第二個最大值。
最小值 (D3) 及其左側對等值剛好落在值域的邊界上,因此最好略過。 |