範例:本徵向量與本徵值
使用 eigenvals、eigenvecs 及 eigenvec 函數求解實數或複數矩陣的本徵值與本徵向量。檢查方形矩陣 M 的理論,若您有滿足下列條件的數字 λ,則非零向量 v 會是 M 的本徵向量:
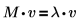
1. 定義輸入方形矩陣。
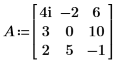
2. 呼叫 eigenvals 與 eigenvecs 求解矩陣 A 的本徵值與本徵向量。
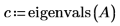
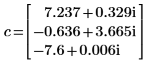
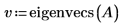

v 的第一欄是對應至 c 第一個元素的本徵向量。同樣地,v 的第二欄是對應於 c 第二個元素的本徵向量,依此類推。
3. 將 v1 定義為第一個本徵向量,並將 c1 定義為 A 的第一個本徵值。比較 A x v1 和 c1 x v1。
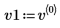
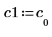
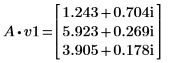 | 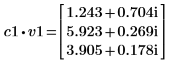 |
4. 將 v2 定義為第一個本徵向量,並將 c2 定義為 A 的第一個本徵值。比較 A x v2 和 c2 x v2。
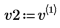
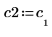
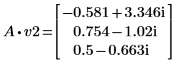 | 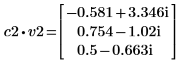 |
5. 將 v3 定義為第一個本徵向量,並將 c3 定義為 A 的第一個本徵值。比較 A x v3 和 c3 x v3。
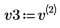
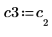
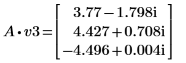 | 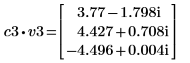 |
6. 呼叫 eigenvec 函數傳回特定本徵值的單一本徵向量。
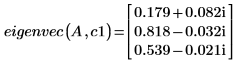

eigenvec 與 eigenvecs 傳回的結果不一定會相符,但都是有效的解。本徵向量不是唯一。它與乘以縮放係數的其他本徵向量相關。若是指定的本徵值,會有不限數目的本徵向量。