範例:縮減取樣向量
使用下列方法從數據向量選擇每第 n 個元素,從第一個元素開始。其可顯示過度縮減取樣的效果 (奈奎斯特定理)。
1. 定義周期與取樣頻率。
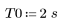
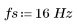
2. 建立信號向量。
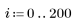
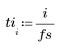
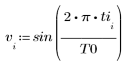
3. 定義長度比向量 v 短的整數 n。
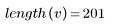
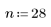
4. 使用向量索引萃取向量 v 的每第 n 個元素。
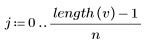
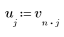
5. 繪製原始與縮減取樣的繪線。
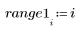
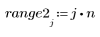
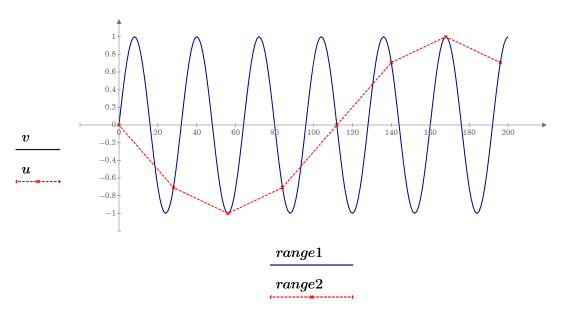
◦ 當新的取樣率太低時 (不經常),信號可能看來失真 (嘗試 n = 15)、完全消失 (僅取樣 0 個點 - 嘗試 n = 16) 或發生混淆現象,亦即信號看來是不正確的頻率 (n = 28,如上所示),因為沒有足夠範例可以精確表示信號中的資訊。
◦ 取樣會針對每個數值演算法而有多個結果,這些結果在離散區間會逼近一個結果,例如快速傅立葉轉換或微分方程式求解器。
◦ 若要適當地縮減取樣信號而不發生混疊現象,在移除每第 n 個點之前,信號必須以 p/n 截止區進行低通濾波。如需詳細資訊,請參閱 Oppenheim 與 Schafer 的 Discrete Time Signal Processing (離散時間信號處理) 第 102-105 頁 (Prentice Hall, ©1989)。