範例:Bessel 函數
使用球體 Bessel 與球體 Hankel 函數以 3D 方井 (原子) 求解薛丁格方程式。
該解代表允許的能量,其中內外波動函數有相等的值與前幾個導數。角度力矩 (L) 的每個值皆有這些能量。
1. 定義質量 (蒲朗克常數),以及原子核半徑:
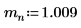
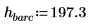
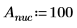
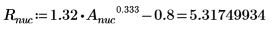
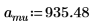
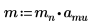
2. 將角度力矩設定為零:
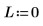
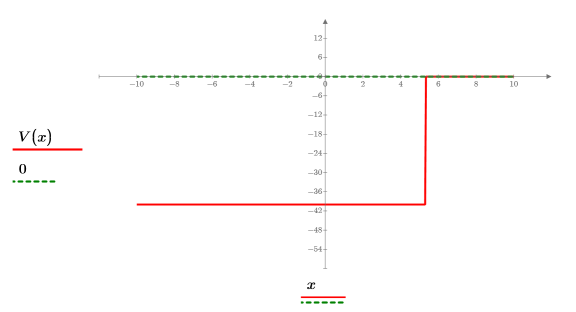
3. 定義及繪製位能井的位能:
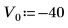
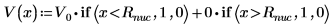
4. 使用球體 Bessel 函數與球體漢克函數求解:
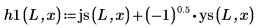
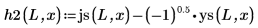
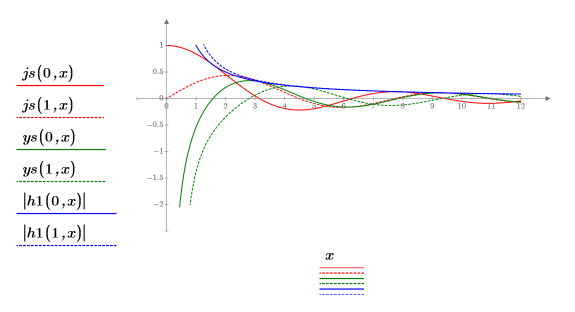
5. 在界定狀態 E < 0 中,為位能井內外第一個能量狀態解,定義波動函數:
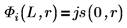
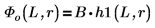
B 是相對正規化。
6. 定義傳播常數:
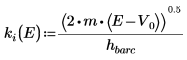
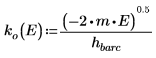
位能井之外的解引數為虛數,因為波動在位能井之外會衰減。
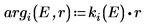
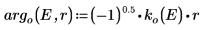
7. 比對位能井邊緣的波動函數 (原子核半徑),決定相對正規化:
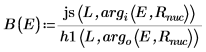
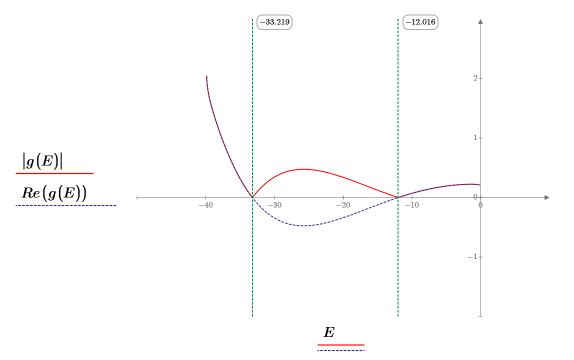
8. 比對導數。尋找導數相等的位置以決定本徵值。
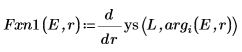
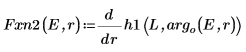
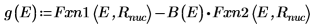
9. 提供 E 的兩個估值:
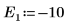
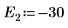
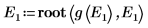
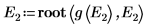
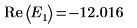
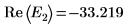
10. 繪製 g(E) 與 E,並新增垂直標記以顯示兩個根點: