示例：方差和标准差

函数 > 统计 > 描述性统计 > 示例：方差和标准差

示例：方差和标准差

使用 Var 和 Stdev 函数对比韦伯分布和正态分布的范围。

1. 定义韦伯分布和正态分布的数据集。

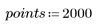
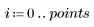
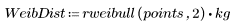
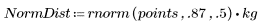
2. 绘制分布图像。

<region id="ID0EEYFAB" top="312" left="0" width="626" height="312" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="0">
          <traceStyle color="#FF00008B" symbol="none" line-weight="1" line-style="Solid">columns</traceStyle>
        </trace>
        <trace resultRef="1">
          <traceStyle color="#FFFF0000" symbol="none" line-weight="1" line-style="Solid">columns</traceStyle>
        </trace>
      </traces>
      <axes>
        <xAxis legend-position="PlotBoundaryBottom" rank="1">
          <axisLine position="origin" positionticmark="0" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat />
          <plotEquations>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <matcol />
                  <id>NormHist</id>
                  <real>0</real>
                </apply>
              </math>
              <math>
                <id label="Unit" xmlns="http://schemas.mathsoft.com/math50">kg</id>
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <matcol />
                  <id>WeibHist</id>
                  <real>0</real>
                </apply>
              </math>
              <math>
                <id label="Unit" xmlns="http://schemas.mathsoft.com/math50">kg</id>
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis legend-position="PlotBoundaryLeft" rank="1">
          <axisLine position="origin" positionticmark="2" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat />
          <plotEquations>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <matcol />
                  <id>NormHist</id>
                  <real>1</real>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <matcol />
                  <id>WeibHist</id>
                  <real>1</real>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

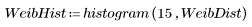
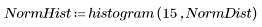
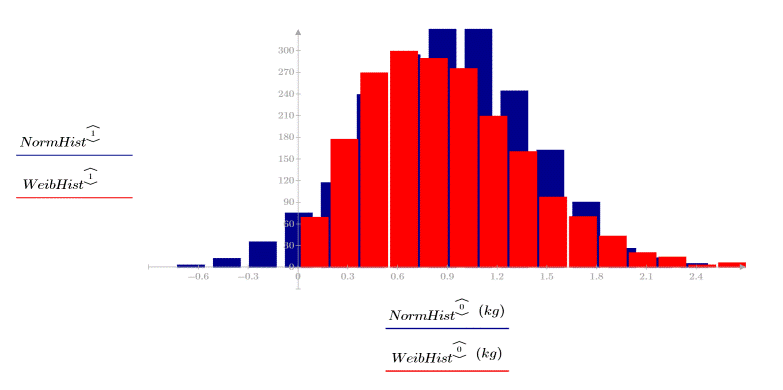
两数据集具有不同的散布和形状，即使它们具有相近的平均值：

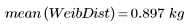
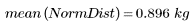
3. 计算分布的样本方差。

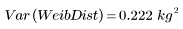
韦伯分布的样本方差较小，表明其散布小于正态分布。

样本方差计算如下：

<region id="ID0EY2FAB" top="1080" left="24" width="394.69" height="67.2973333333333" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math>
    <define xmlns="http://schemas.mathsoft.com/math50">
      <function>
        <id label="None">Variance</id>
        <boundVars>
          <id label="None">V</id>
        </boundVars>
      </function>
      <apply>
        <mult />
        <apply>
          <div />
          <real>1</real>
          <apply>
            <minus />
            <apply>
              <id>rows</id>
              <id>V</id>
            </apply>
            <real>1</real>
          </apply>
        </apply>
        <parens>
          <apply>
            <summation />
            <lambda>
              <boundVars>
                <id>i</id>
              </boundVars>
              <apply>
                <pow />
                <parens>
                  <apply>
                    <minus />
                    <apply>
                      <indexer />
                      <id>V</id>
                      <id>i</id>
                    </apply>
                    <apply>
                      <id>mean</id>
                      <id>V</id>
                    </apply>
                  </apply>
                </parens>
                <real>2</real>
              </apply>
            </lambda>
            <lowerBound>
              <real>0</real>
            </lowerBound>
            <upperBound>
              <apply>
                <minus />
                <apply>
                  <id>rows</id>
                  <id>V</id>
                </apply>
                <real>1</real>
              </apply>
            </upperBound>
          </apply>
        </parens>
      </apply>
    </define>
    <resultFormat>
      <decimal precision="round-trip-decimal-places" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
      <matrix size="12,12" offset="0,0" show-indices="false" />
    </resultFormat>
  </math>
</region>

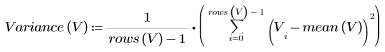
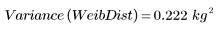
4. 计算韦伯分布的样本标准差。

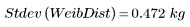
该标准差具有与原始数据相同的单位，因此离差的测量比方差稍微直观一些。它可以被视为理论上应该保持一致的一系列测量值中对误差的测量。

样本标准差是样本方差的平方根：

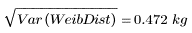
5. 计算韦伯分布的总体方差和标准差：

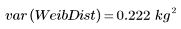
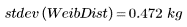
总体方差和标准差除以样本大小，而不除以样本大小减一：

<region id="ID0E3AGAB" top="1584" left="24" width="369.073333333333" height="67.2973333333333" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math>
    <define xmlns="http://schemas.mathsoft.com/math50">
      <function>
        <id label="None">variance</id>
        <boundVars>
          <id label="None">V</id>
        </boundVars>
      </function>
      <apply>
        <mult />
        <apply>
          <div />
          <real>1</real>
          <apply>
            <id>rows</id>
            <id>V</id>
          </apply>
        </apply>
        <parens>
          <apply>
            <summation />
            <lambda>
              <boundVars>
                <id>i</id>
              </boundVars>
              <apply>
                <pow />
                <parens>
                  <apply>
                    <minus />
                    <apply>
                      <indexer />
                      <id>V</id>
                      <id>i</id>
                    </apply>
                    <apply>
                      <id>mean</id>
                      <id>V</id>
                    </apply>
                  </apply>
                </parens>
                <real>2</real>
              </apply>
            </lambda>
            <lowerBound>
              <real>0</real>
            </lowerBound>
            <upperBound>
              <apply>
                <minus />
                <apply>
                  <id>rows</id>
                  <id>V</id>
                </apply>
                <real>1</real>
              </apply>
            </upperBound>
          </apply>
        </parens>
      </apply>
    </define>
    <resultFormat>
      <decimal precision="round-trip-decimal-places" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
      <matrix size="12,12" offset="0,0" show-indices="false" />
    </resultFormat>
  </math>
</region>

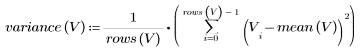
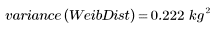
样本方差或函数 Var 是在量化数据分析中更为常用的定义。