示例:有理函数回归 1
rationalfit
使用 rationalfit 函数将有理多项式拟合到数据。
1. 定义数据集。

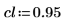
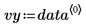
此数据集来自半导体电子迁移率的 NIST 研究。预测变量 vx 是密度的自然对数。响应变量 vy 是电子迁移率的测量值。
2. 指定有理函数分子和分母的阶数。

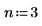
拟合函数具有下列形式:
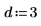
3. 定义置信限。
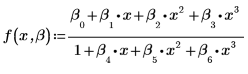
4. 调用 rationalfit 函数。
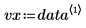
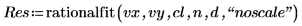
输出的第一列包含参数的值。第二列和第三列分别包含置信下限和置信上限的输出。
5. 将参数的值与在 NIST 网站找到的正确值进行比较。


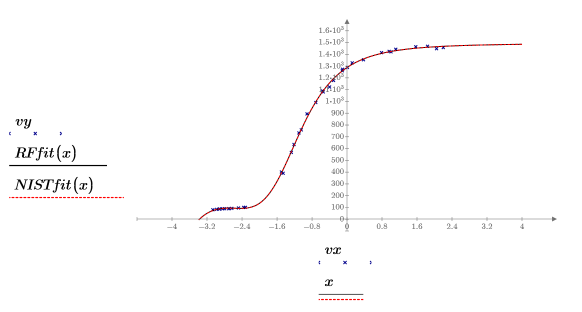
6. 绘制数据、有理函数回归以及 NIST 参数定义的拟合。

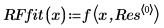
通过下面的相关系数可确认,有理函数回归的拟合几近完美:
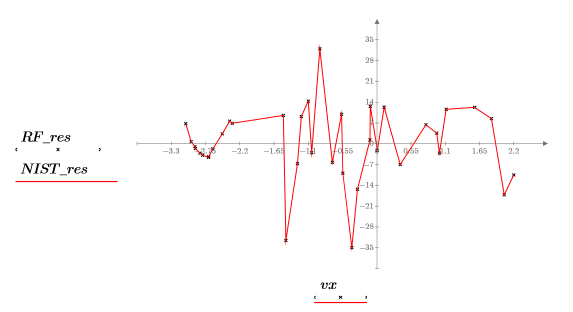
残差图
创建残差图以显示上述回归的拟合度。
1. 定义自由度。
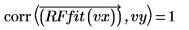
2. 计算残差。
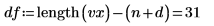
3. 计算残差的平方和。
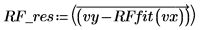
4. 计算标准差。
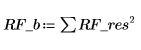
5. 使用 NIST 网站中的值重复步骤 2 到 4。
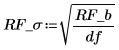
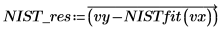
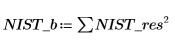
6. 比较两个拟合的结果。
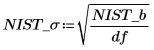
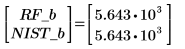
7. 绘制数据点和残差。
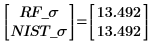
约束、标准差和公差
可以为 rationalfit 选择多个自变量:标准差矢量、矩阵下界和上界、精度以及 "no scale"。可以单独使用任意一个可选自变量,但对于上面定义的前三个自变量,必须考虑自变量的阶。
1. 创建参数的下界和上界矩阵。
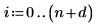
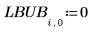
2. 创建参数的标准差矢量。
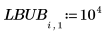
将标准差矢量作为自变量输入到 rationalfit 函数时,求解器会求解下列函数的最小值:
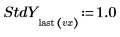
如果某个点的标准差为 0,则在该点使用原始的无偏差函数,即,StdYi 设置为 1。
3. 设置精度。默认值为 10-7。
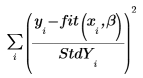
4. 4. 调用 rationalfit 函数。将返回的参数值与 NIST 网站中的正确值加以比较。
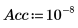
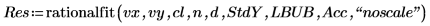
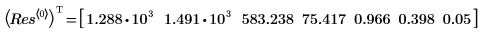
rationalfit 函数在该输入数据上进行自动换算,以便精度可保持标度不变。然后会重新调整输出参数的标度以匹配原始数据。大多数情况下,可确保实现拟合,无论输入数据的相对标度为何。如果未正常实现理想拟合,则可在自变量列表末尾添加 “noscale” 选项字符串,以关闭此选项。