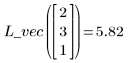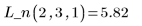示例:分段二次拟合
一元多项式回归
使用局部回归,通过 loess 函数将系列二次函数拟合到数据。
1. 定义下面的矩阵:

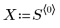
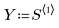
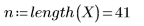
2. 在每个数据点周围的加权窗中,定义总点数的跨度或百分比,loess 函数可使用它进行连续二次拟合。
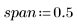
由于希望将大于 1 的点平均分布在每个最小二乘拟合中,因此基本准则是 (span*n) 应大于 1:
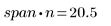
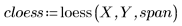
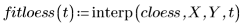
4. 调用 polyfit 函数将二阶多项式拟合到数据集。
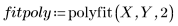
5. 绘制以上两条已定义曲线的图像。
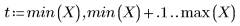
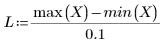
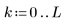
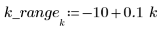
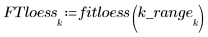
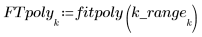
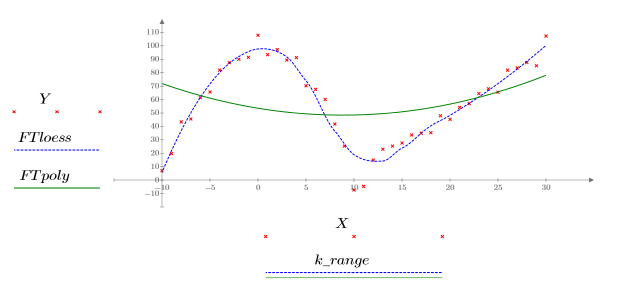
• 当跨度很大 (例如,2 或 3) 时,数据将被视为是权重几乎相等的单一二次拟合。该拟合趋于二次多项式的 polyfit 解。
• 对于如何选取跨度并没有确切的准则。随着跨度的增大,loess 拟合的绘图会变得更平滑,因为拟合中连接的分段越来越少。但是,拟合可能无法恰当地遵循数据特征。相反,随着跨度的减小,可能会发现 loess 并不收敛。
• loess 算法不适用于外插法。如果试图使用超出原始 x 范围的值计算 interp,将会返回错误。
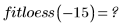
• 当数据具有某些不连续性特征,但又不希望进行手动分段拟合或使用在实际中难以实现的非线性复杂拟合方法时,可使用 loess。
多变量多项式回归
使用 loess 函数实现多变量多项式回归。loess 函数不能拟合四个以上的独立变量。
1. 定义数据集。
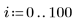
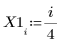
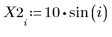
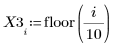
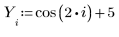
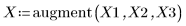
2. 定义平滑参数。
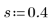
此参数与一个因子的情况具有相同的含义。
3. 调用 loess 函数。
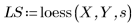
4. 调用 interp 插入多变量拟合函数。该拟合函数可使用具有 n 个元素的矢量或具有 n 个自变量的矢量集,其中 n 为独立因子的数量。
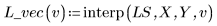
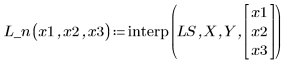
5. 使用拟合函数预测 Y 在点 (2, 3, 1) 处的值。