示例:位置估值器
mean
求出数据集的算术平均数。
1. 定义数字数据集。

2. 使用 mean 函数来计算数据的算术平均值。
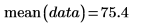
这等同于下列计算:
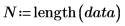
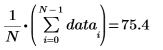
3. 计算该均值之前更改其中的一个数据点。
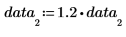
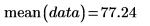
均值对于一个或多个数据点数值的改变是敏感的。如果数据集具有明显的离群值,您会发现其均值并不能理想地描述中心位置。您可以对离群值进行修剪,然后计算修剪的均值,从而获得更好的估计值。
median
求出数据集的中值或中间值。
1. 使用 median 函数求出上一个数据集的中值。
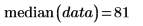
2. 使用 sort 函数按升序排列的数据进行排序并证明中值正是集的中间值:
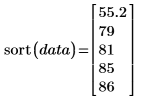
中值取决于数据的相对位置,而不是每个数据点的实际值。因此,中值对于个别数据值的改变相对而言并不敏感。
3. 使用 median 函数求出偶数个数据点的中值。
 | 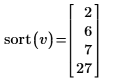 | 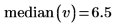 |
当数据集包含偶数个数据点时,中值为中间两个数据点的平均值。
mode
众数是指数据集中出现频率最高的数值。
1. 使用 mode 函数求出数据集的模式。由于数据集中没有重复的数值,则会返回错误。


2. 创建一个包含多个以相同频率重复的元素的新数据集。
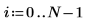 | 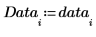 | 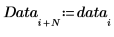 |
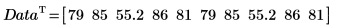 | ||
3. 使用 mode 函数证明,当多个数据值以相同频率重复时,将返回错误。

percentile
使用 percentile 函数求出数据集的百分位数、四分位数及中值。百分位数可测量数据集中的哪些值落于数据点总数量的某个百分比之下。
1. 定义数据集。
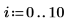
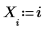
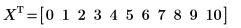
2. 使用 percentile 函数求出数据集 X 的第五十个百分位数。
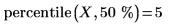
这等同于数据集 X 的中值:
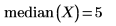
3. 使用 percentile 函数求出数据集 X 的第九十个百分位数。
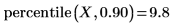
第九十个百分位数出现在两数据点之间。
4. 使用 percentile 函数求出第一个数据集的四分位数。
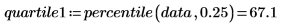
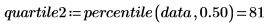
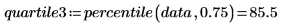
四分位数是依次标记 1/4 数据的三个百分位数之一。四分位数可在“分位数-分位数”图中用于数据的图形分析。