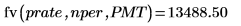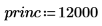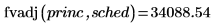函数 > 金融 > 示例：金融函数
示例：金融函数
1. 定义年利率：
单击可复制此表达式
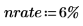
2. 定义每年的复利计算期数：
单击可复制此表达式
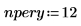
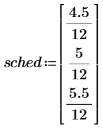
3. 定义期利率：
单击可复制此表达式
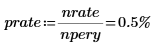
4. 定义复利计算期数：
单击可复制此表达式
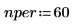
5. 定义贷款的现值和未来价值：
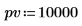
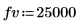
单击可复制此表达式
单击可复制此表达式
付款
1. 使用 pmt 函数计算所需的月付款以付清 10,000 元的贷款 (利率为 6%，期限为 5 年)：
单击可复制此表达式
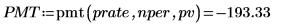
输入对贷款的付款额，其显示为负数。
2. 使用 ppmt 函数计算上述贷款第 36 个月的本金付款额：
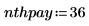
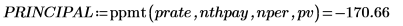
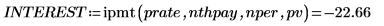
单击可复制此表达式
单击可复制此表达式
3. 使用 ipmt 函数计算上述贷款第 36 个月的利息付款额：
单击可复制此表达式
本金付款额加上利息付款额为付款总额 PMT。
单击可复制此表达式
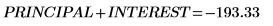
累计利息、累计本金及 APR
1. 使用 cumint 函数计算针对上述贷款已付的累计利息：
单击可复制此表达式
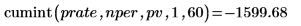
2. 使用 cumprn 函数计算针对上述贷款已付的累计本金：
单击可复制此表达式
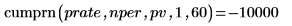
3. 使用 eff 函数计算针对上述贷款已付的有效年利率 (APR)：
单击可复制此表达式
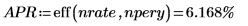
利率
1. 给定现值 pv 及复利计算期数 nper，使用 crate 函数计算一笔用于产生未来价值 fv 的投资的每期固定利率。
单击可复制此表达式
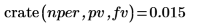
返回的值为每期或每月的利率。这对应于 18% 的年利率。
2. 使用 nom 函数计算对应于上述年利率 (APR) 的名义利率：
单击可复制此表达式
3. 给定周期固定付款 pmt 和 pv 现值，使用 rate 函数计算基于 nper 复利计算期数的贷款的每期利率。
单击可复制此表达式
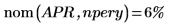
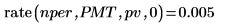
返回的值为每期或每月的利率。这对应于 6% 的年利率。
期数
1. 假设您赚取 prate 的年利率，使用函数 cnper 计算要达到 pv 的投资 fv 的复利计算期数：
单击可复制此表达式
2. 假设您每月付款 并且赚取 nper 的年利率，使用函数 pvfv 计算要达到 PMT 的一笔投资 prate 的周期数：
单击可复制此表达式
未来价值
1. 基于周期固定付款 PMT、针对复利计算期数 nper 以及使用固定利率 prate，使用 fv 函数计算投资的未来价值。
单击可复制此表达式
2. 应用连续复合利率 sched 后，使用 fvadj 函数计算初始本金 princ 的未来价值。
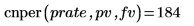
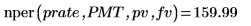
单击可复制此表达式
单击可复制此表达式
单击可复制此表达式
3. 使用 fvc 函数计算在均匀间隔下赚取利率 prate 的连续现金流的未来价值。
单击可复制此表达式
单击可复制此表达式
关于金融函数
这对您有帮助吗?