示例:倒谱和复倒谱
倒谱可将卷积和去卷积映射为频域中的加法和减法,可应用于语音和地球物理学的信号处理。
cepstrum
序列 x(n) 的倒谱由下述公式指定:
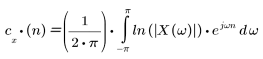
其中,X(ω) 是序列 x(n) 的傅立叶变换。
这是对 x(n) 的傅立叶变换取自然对数后的逆变换的定义。取对数可将时域中的卷积映射为频域中的加法,使得倒谱成为方便的信号去卷积 (映射为减法) 工具。
1. 定义 n 的范围。
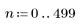
2. 定义序列函数 x。
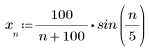
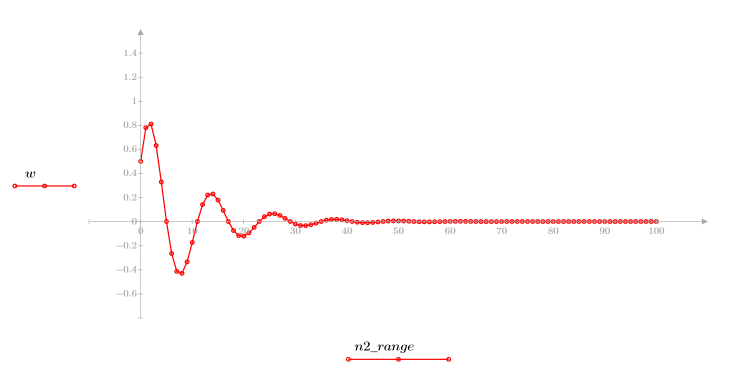
3. 绘制序列函数 x 的图像。
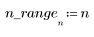
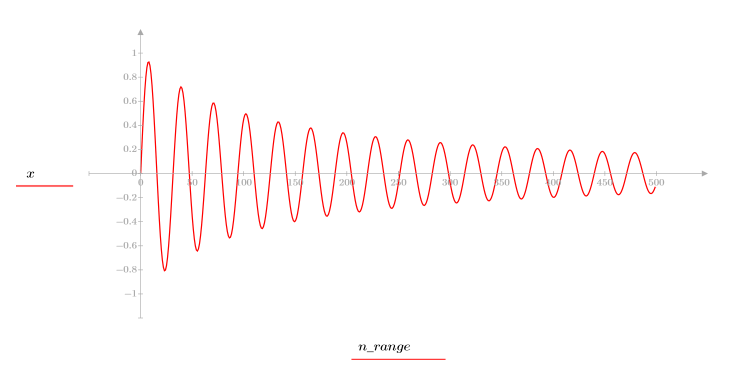
4. 计算倒谱并绘制生成的函数的图像。
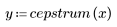
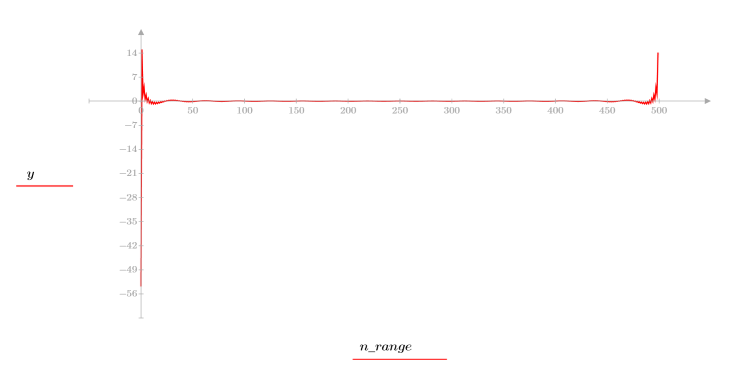
5. 使用 recenter 函数重新居中结果,以使第一个元素成为中间元素。
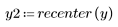
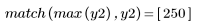
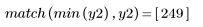
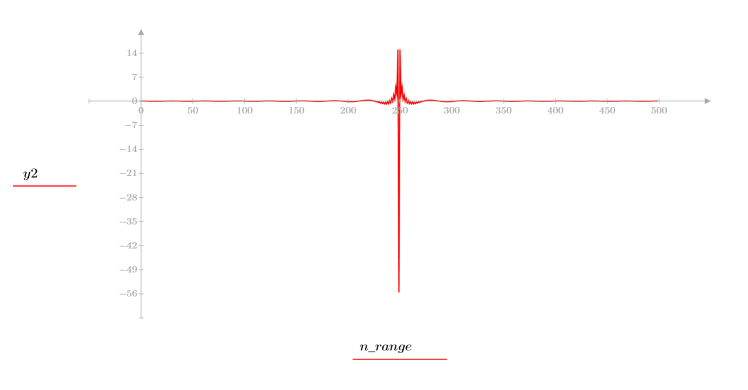
不能从倒谱恢复原始信号,因为相位信息未保留。
ccepstrum
复倒谱函数由下述复对数指定。
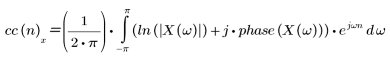
其中,X(ω) 是序列 x(n) 的傅立叶变换,phase 用于捕获给定序列的相位信息。
如果将输出信号的复倒谱与输入和通道序列的复倒谱进行比较,会发现输出的复倒谱是输入和通道的复倒谱之和。这与在频域中添加两种信号的谱类似,但前者是在时域中完成的。
下面的示例所模拟的信号为通信通道中的信号,该通信通道将产生回声 (请参照 Oppenheim and Schaefer, Prentice-Hall, 1989 的 12.8.1 小节)。
1. 定义并绘制 FIR 滤波器的通道响应,该滤波器引入了另一个序列 (回声) 的衰减副本。
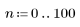
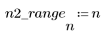
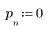
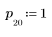
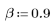
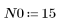
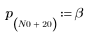
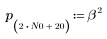
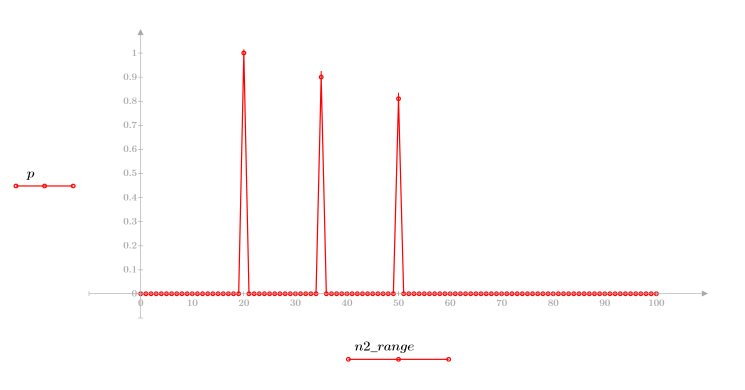
2. 定义并绘制将与通道响应进行卷积运算的序列 v。
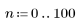
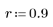
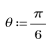
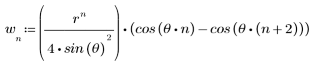
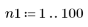
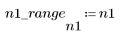
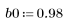
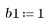
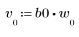
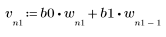
3. 使用 response 函数获取使用系数数组 v (通信通道函数 v) 的 FIR 滤波器的输入矢量 p 的 n 项矢量响应。
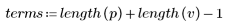
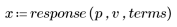
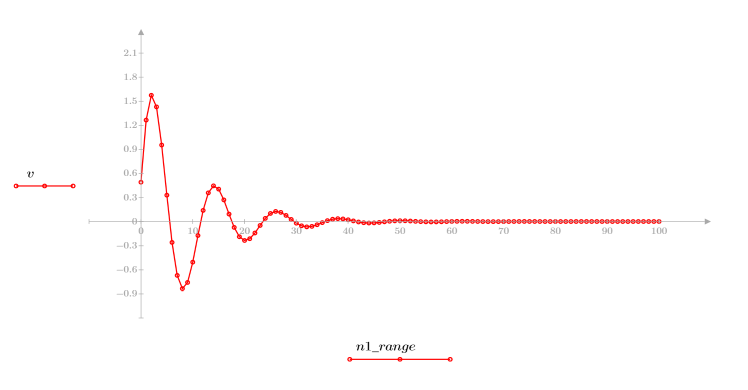
4. 绘制响应函数图像。
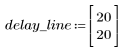
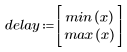
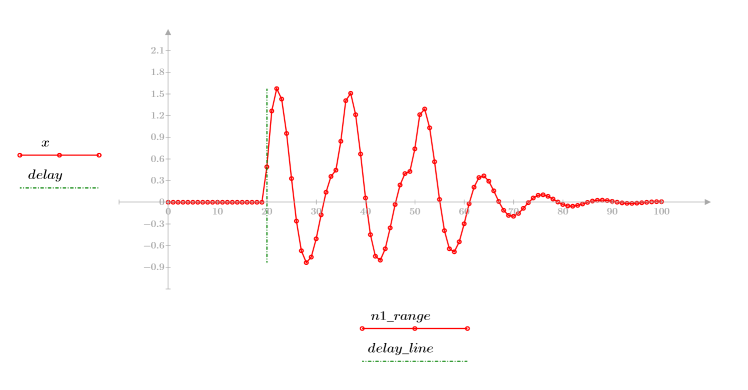
◦ 生成的序列是输入函数 p 和通信通道函数 v 的卷积。
◦ 该序列显示原始信号与延迟的副本。
5. 将输出信号的复倒谱与原始序列的倒谱进行比较。使结果回到中心位置以便于比较。
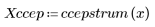
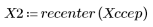
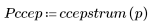
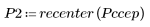
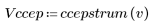
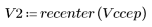
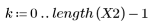
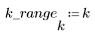
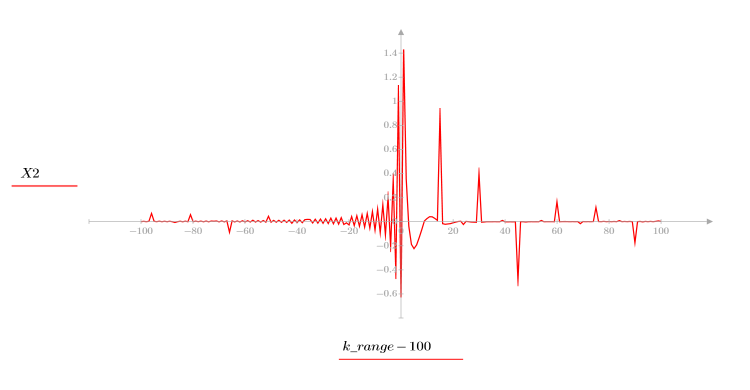
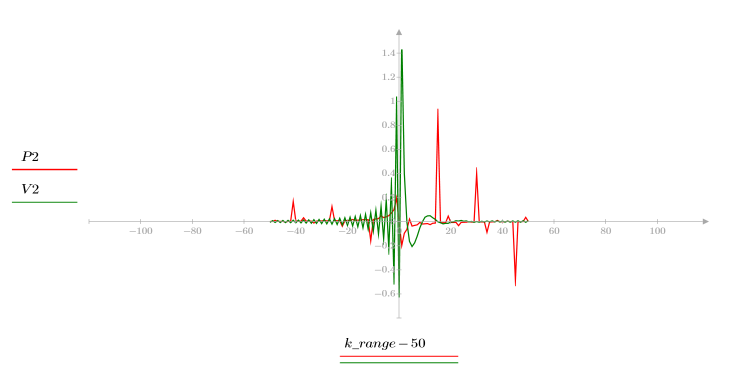
上面的绘图显示输出信号的复倒谱是进行卷积运算的两个序列的复倒谱之和。